Fonction composée avec radical, exponentielle et arcsin
Colle de mathématiques
Sujet de colle de maths:- DérivéeEtude de fonctions (dérivée, continuité, variations, limites, ...)
Énoncé du sujet
- Pour quelles valeurs de
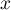 a-t-on
a-t-on  ?
?
- Etudier la fonctions
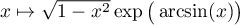 .
.
Correction
Correction
-
 existe seulement pour
existe seulement pour  ,
et
,
et 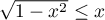 ne peut être vraie que pour
ne peut être vraie que pour 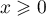 ,
donc pour
,
donc pour ![$x\in[0;1]$](/Generateur-Devoirs/Colles/Calcul/exarcsin3_c/5.png) .
.
On peut alors poser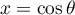 avec
avec  ,
et alors
,
et alors
 .
.
On trouve alors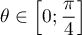 et
donc
et
donc 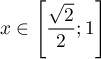 car
car 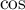 est décroissante
sur
est décroissante
sur ![$[0;\pi]$](/Generateur-Devoirs/Colles/Calcul/exarcsin3_c/12.png) .
.
- Pour
 ,
,
Remarquons déjà qu'on se limite à![$x\in[-1,1]$](/Generateur-Devoirs/Colles/Calcul/exarcsin3_c/14.png) , pour que
, pour que  ait un sens. Il est aussi clair que l'inégalité n'est pas vérifiée si
ait un sens. Il est aussi clair que l'inégalité n'est pas vérifiée si 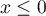 . On se restreint donc à
. On se restreint donc à ![$x\in[0,1]$](/Generateur-Devoirs/Colles/Calcul/exarcsin3_c/17.png) , et, puisque tout est positif, on a
, et, puisque tout est positif, on a
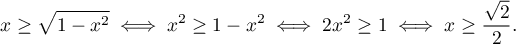
L'inégalité est donc vérifiée si et seulement si![$x\in\left[\frac{\sqrt 2}2,1\right]$](/Generateur-Devoirs/Colles/Calcul/exarcsin3_c/19.png) .
.
- Remarquons d'abord que la fonction
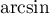 est définie sur
est définie sur ![$[-1,1]$](/Generateur-Devoirs/Colles/Calcul/exarcsin3_c/21.png) , et que pour ces valeurs de
, et que pour ces valeurs de 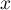 ,
,  est également bien définie. Le domaine de
définition de
est également bien définie. Le domaine de
définition de  est donc
est donc ![$[-1,1]$](/Generateur-Devoirs/Colles/Calcul/exarcsin3_c/25.png) . De plus,
. De plus,  est dérivable sur
est dérivable sur ![$]-1,1[$](/Generateur-Devoirs/Colles/Calcul/exarcsin3_c/27.png) , et on a
, et on a
![\[\begin{array}{lcl}
f'(x)&=&\dsp\frac{-2x}{2\sqrt{1-x^2}}e^{\arcsin x}+\sqrt{1-x^2}\times\frac 1{\sqrt{1-x^2}}e^{\arcsin x}\\[1.8em]
&=&\dsp\lp\frac{-x}{\sqrt{1-x^2}}+1\right)e^{\arcsin x}\\[1.8em]
&=&\dsp\frac{-x+\sqrt{1-x^2}}{\sqrt{1-x^2}}e^{\arcsin x}.
\enar\]](/Generateur-Devoirs/Colles/Calcul/exarcsin3_c/28.png)
La question précédente nous donne le signe de la dérivée, et on en déduit le tableau de variations :
![\[\begin{tabular}{|c|ccccc|}\hline
$x$ & $-1$ && $\dfrac{\sqrt2}{2}$ && 1 \\\hline
$f'(x)$ &&$+$&0&$-$&\\\hline
&&&&&\\
$f$ &&\Large{$\nearrow$}&&\Large{$\searrow$}&\\
&0&&&&0\\\hline
\end{tabular}\]](/Generateur-Devoirs/Colles/Calcul/exarcsin3_c/29.png)
La courbe représentative de la fonction est:
![\[\psset{xunit=3cm,yunit=2cm,arrowsize=7pt}
\begin{pspicture}(-1,-1)(1,2)
\psline{->}(-1.3,0)(1.3,0)
\psline{->}(0,-.4)(0,2)
\psplot[plotpoints=1000]{-1}{1}{1 x 2 exp sub .5 exp 2.718 x arcsin 3.14 mul 180 div exp mul}
\rput(-.1,-.15){$0$}
\psline(-1,-.05)(-1,.05)\rput(-1,-.15){$-1$}
\psline(1,-.05)(1,.05)\rput(1,-.15){$1$}
\psline(-.05,1)(.05,1)\rput(-.15,1){$1$}
\end{pspicture}\]](/Generateur-Devoirs/Colles/Calcul/exarcsin3_c/30.png)
Tag:Dérivée
Autres sujets au hasard:

Voir aussi: