Raccordement dérivable
Colle de mathématiques
Sujet de colle de maths:- DérivéeEtude de fonctions (dérivée, continuité, variations, limites, ...)
Énoncé du sujet
Soit ![$f:[0,1]\to\mathbb R$](/Generateur-Devoirs/Colles/Calcul/exraccordement-derivable/1.png) dérivable vérifiant
dérivable vérifiant 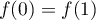 avec
avec 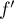 continue en
continue en 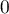 et en
et en  . On définit
. On définit 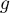 sur
sur ![$[0,1]$](/Generateur-Devoirs/Colles/Calcul/exraccordement-derivable/7.png) par
par
![\[g(x)=\la\begin{array}{lll}
f(2x)&\text{ si }&0\leq x\leq\dfrac12\\
f(2x-1)&\text{ si }&\dfrac12\leqslant x\leq 1.
\enar\right.\]](/Generateur-Devoirs/Colles/Calcul/exraccordement-derivable/8.png)
 est-elle continue? dérivable? Si non, quelle(s) hypothèse(s) faut-il ajouter pour que ce soit le cas?
est-elle continue? dérivable? Si non, quelle(s) hypothèse(s) faut-il ajouter pour que ce soit le cas?
![\[g(x)=\la\begin{array}{lll}
f(2x)&\text{ si }&0\leq x\leq\dfrac12\\
f(2x-1)&\text{ si }&\dfrac12\leqslant x\leq 1.
\enar\right.\]](/Generateur-Devoirs/Colles/Calcul/exraccordement-derivable/8.png)
Correction
 est continue et dérivable sur
est continue et dérivable sur ![$]0,1/2[$](/Generateur-Devoirs/Colles/Calcul/exraccordement-derivable_c/2.png) et sur
et sur ![$]1/2,1[$](/Generateur-Devoirs/Colles/Calcul/exraccordement-derivable_c/3.png) , comme composée de fonctions qui le sont:
, comme composée de fonctions qui le sont:  ,
,  et
et  .
Le seul problème est éventuellement en 1/2.
.
Le seul problème est éventuellement en 1/2.
On a
![\[\lim_{x\to \frac{1}2^-}g(x)=f(1)\]](/Generateur-Devoirs/Colles/Calcul/exraccordement-derivable_c/7.png)
et
![\[\lim_{x\to \frac12^+}g(x)=f(0)\]](/Generateur-Devoirs/Colles/Calcul/exraccordement-derivable_c/8.png)
et, comme , la fonction
, la fonction  est donc continue en 1/2.
est donc continue en 1/2.
Pour , on a
, on a
![\[g'(x)=2f'(2x)\begin{minipage}[t]{4em}$\ \longrightarrow$\\\scriptsize$x\to \frac 12^-$\end{minipage} 2f'(1)\]](/Generateur-Devoirs/Colles/Calcul/exraccordement-derivable_c/12.png)
et donc, par le théorème de prolongement d'une dérivée, admet une dérivée à gauche en 1/2 égale à
admet une dérivée à gauche en 1/2 égale à  .
.
De même, pour , on a
, on a
![\[g'(x)=2f'(2x-1)\begin{minipage}[t]{4em}$\ \longrightarrow$\\\scriptsize$x\to \frac 12^+$\end{minipage} 2f'(0)\]](/Generateur-Devoirs/Colles/Calcul/exraccordement-derivable_c/16.png)
et donc, par le théorème de prolongement d'une dérivée, admet une dérivée à droite en 1/2 égale à
admet une dérivée à droite en 1/2 égale à  .
.
Maintenant, la fonction est dérivable en 1/2 si et seulement si les dérivées à droite et à gauche sont égales, c'est-à-dire si et seulement
est dérivable en 1/2 si et seulement si les dérivées à droite et à gauche sont égales, c'est-à-dire si et seulement  .
.
Correction
La fonctionOn a
et
et, comme
Pour
et donc, par le théorème de prolongement d'une dérivée,
De même, pour
et donc, par le théorème de prolongement d'une dérivée,
Maintenant, la fonction
Tag:Dérivée
Autres sujets au hasard:

Voir aussi: