Équation polynomiale de degré 4
Colle de mathématiques
Sujet de colle de maths:Énoncé du sujet
Résoudre dans  , puis dans
, puis dans 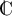 , l'équation:
, l'équation:
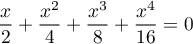
Correction
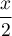 et donc, pour
et donc, pour 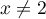 (mais de toute façon,
(mais de toute façon,  n'est pas solution),
n'est pas solution),
![\[\dfrac{x}{2}+\dfrac{x^2}{4}+\dfrac{x^3}{8}+\dfrac{x^4}{16}
=\dfrac{x}{2}\dfrac{1-\lp\dfrac{x}{2}\rp^4}{1-\dfrac{x}{2}}
\]](/Generateur-Devoirs/Colles/Complexes/exEqdeg4.1_c/4.png)
et donc, dans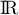 ,
,
 si et seulement si
si et seulement si
 ou
ou 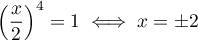 .
.
 n'est pas solution, et
donc, dans
n'est pas solution, et
donc, dans 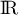 , l'équation a deux solutions
, l'équation a deux solutions  et
et  .
.
Dans , on a la même factorisation, mais par contre
, on a la même factorisation, mais par contre
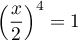 pour
pour 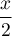 racine quatrième de l'unité,
soit
racine quatrième de l'unité,
soit
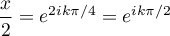 , pour
, pour 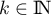 ,
, 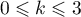 ,
et donc l'équation admet 4 solutions (
,
et donc l'équation admet 4 solutions ( n'est toujours pas solution...):
n'est toujours pas solution...):
![\[\mathcal{S}=\la0;\, 2i,\, -2,\, -2i \ra\]](/Generateur-Devoirs/Colles/Complexes/exEqdeg4.1_c/20.png)
Correction
Il s'agit de la somme de termes en progression géométrique, de raison![\[\dfrac{x}{2}+\dfrac{x^2}{4}+\dfrac{x^3}{8}+\dfrac{x^4}{16}
=\dfrac{x}{2}\dfrac{1-\lp\dfrac{x}{2}\rp^4}{1-\dfrac{x}{2}}
\]](/Generateur-Devoirs/Colles/Complexes/exEqdeg4.1_c/4.png)
et donc, dans
Dans
Tags:ComplexesSommes
Autres sujets au hasard:

Voir aussi: