Endomorphisme de polynômes
Colle de mathématiques
Sujet de colle de maths:- Applications linéairesApplications linéaires
Énoncé du sujet
oral HEC, BL - 2022.
On note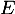 l'espace vectoriel des fonctions polynomiales de degré inférieur ou égal à 2. On définit les fonctions
l'espace vectoriel des fonctions polynomiales de degré inférieur ou égal à 2. On définit les fonctions 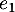 ,
, 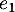 ,
, 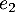 par:
par:
![\[e_0(t) = 1 ,\ e_1(t) = t , \ e_2 (t) = t^2\]](/Generateur-Devoirs/Colles/Applin/HEC-BL-2022-4.1/5.png)
pour tout réel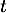 .
.
On rappelle que la famille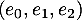 est une base de
est une base de 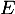 .
On considère l'application
.
On considère l'application 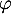 qui, à toute fonction
qui, à toute fonction 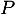 de
de 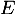 , associe la fonction, notée
, associe la fonction, notée 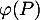 , définie par:
, définie par:
![\[\forall x\in\R,
\varphi(P)(x)=\int_0^1P(x+t)dt\]](/Generateur-Devoirs/Colles/Applin/HEC-BL-2022-4.1/13.png)
On note
pour tout réel
On rappelle que la famille
- Question de cours : Critère d'inversibilité d'une matrice triangulaire.
- Montrer que
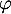 est un endomorphisme de
est un endomorphisme de 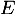 .
.
-
- Écrire la matrice
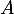 de
de 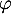 dans la base
dans la base 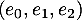 .
.
- Justifier que
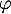 est un automorphisme de
est un automorphisme de 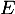 .
.
- L'endomorphisme
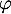 est-il diagonalisable?
est-il diagonalisable?
- Écrire la matrice
-
- Montrer que pour tout entier naturel
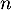 , il existe un réel
, il existe un réel 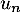 tel que:
tel que:
![\[A^n=\lp\begin{array}{ccc}1&\frac{n}2&u_n\\0&1&n\\0&0&1\enar\rp\]](/Generateur-Devoirs/Colles/Applin/HEC-BL-2022-4.1/24.png)
- En déduire, par sommation, l'expression de
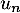 pour tout entier
pour tout entier 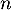 .
.
- Montrer que pour tout entier naturel
Correction
Correction
oral HEC, BL - 2022 - Exercice avec préparation- Une matrice est inversible si et seulement si 0 n'est pas valeur propre.
Or une matrice triangulaire a ses valeurs propres directement sur sa diagonale.
Ainsi, une matrice triangulaire est inversible si et seulement ses coefficients diagonaux sont tous non nuls.
- La linéarité de
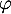 découle directement de la linéarité de l'intégrale.
En effet, soit
découle directement de la linéarité de l'intégrale.
En effet, soit 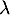 et
et 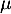 deux réels et
deux réels et 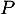 et
et 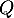 deux polynômes de
deux polynômes de 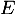 , alors, pour tout réel
, alors, pour tout réel 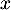 ,
,
![\[\begin{array}{ll}\varphi(\lambda P+\mu Q)(x)&=\dsp\int_0^1\biggl(\lambda P+\mu Q\biggr)(x+t)dt\\
&=\dsp\int_0^1\biggl(\lambda P(x+t)+\mu Q(x+t)\biggr)dt\\
&=\dsp\lambda\int_0^1P(x+t)+\mu \int_0^1Q(x+t))dt\\
&=\lambda\varphi(P)(x)+\mu\varphi(Q)(x)\enar\]](/Generateur-Devoirs/Colles/Applin/HEC-BL-2022-4.1_c/8.png)
c'est-à-dire que
![\[\varphi(\lambda P+\mu Q)=\lambda\varphi(P)+\mu\varphi(Q)\]](/Generateur-Devoirs/Colles/Applin/HEC-BL-2022-4.1_c/9.png)
et cette application est donc bien linéaire.
Il reste maintenant à montrer que pour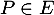 , on a aussi
, on a aussi 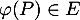 .
.
On peut le montrer on prenant un polynôme quelconque de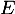 , soit
, soit 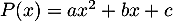 , et calculer
, et calculer 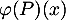 .
.
Plus simplement, on peut mettre à profit la linéarité que l'on veint de démontrer et donc séparer le calcul précédent en les calculs de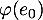 ,
, 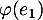 et
et 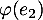 .
.
On a
![\[\varphi(e_0)(x)=\int_0^11dt=1\]](/Generateur-Devoirs/Colles/Applin/HEC-BL-2022-4.1_c/18.png)
puis
![\[\begin{array}{ll}\varphi(e_1)(x)&=\dsp\int_0^1(x+t)dt\\
&=\left[ xt+\dfrac12t^2\rb_0^1\\
&=x+\dfrac12\enar\]](/Generateur-Devoirs/Colles/Applin/HEC-BL-2022-4.1_c/19.png)
et enfin
![\[\begin{array}{ll}\varphi(e_2)(x)&=\dsp\int_0^1(x+t)^2dt\\
&=\dsp\int_0^1\left( x^2+2xt+t^2\right) dt\\
&=x^2+x+\dfrac13\enar\]](/Generateur-Devoirs/Colles/Applin/HEC-BL-2022-4.1_c/20.png)
On trouve ainsi que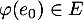 ,
, 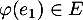 , et
, et
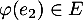 , et donc, par linéarité, pour tout
, et donc, par linéarité, pour tout 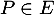 , on a
, on a
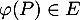 , c'est-à-dire que
, c'est-à-dire que 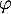 est un endomorphisme de
est un endomorphisme de 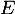 .
.
-
- D'après les calculs précédents, on a trouvé que
![\[\varphi(e_0)=e_0\]](/Generateur-Devoirs/Colles/Applin/HEC-BL-2022-4.1_c/28.png)
et
![\[\varphi(e_1)=e_1+\dfrac12e_0\]](/Generateur-Devoirs/Colles/Applin/HEC-BL-2022-4.1_c/29.png)
et
![\[\varphi(e_2)=e_2+e_1+\dfrac13e_0\]](/Generateur-Devoirs/Colles/Applin/HEC-BL-2022-4.1_c/30.png)
On a donc la matrice de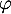 dans la base
dans la base 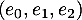 ,
,
![\[A=\lp\begin{array}{ccc}1&1/2&1/3\\0&1&1\\0&0&1\enar\rp\]](/Generateur-Devoirs/Colles/Applin/HEC-BL-2022-4.1_c/33.png)
- La matrice
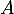 est triangulaire supérieure, et d'après la question de cours, on sait ici qu'elle est donc inversible, et l'application
est triangulaire supérieure, et d'après la question de cours, on sait ici qu'elle est donc inversible, et l'application 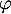 est donc un automorphisme.
est donc un automorphisme.
- Les valeurs propres de
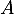 sont sur sa diagonale: 1 est l'unique valeur propre de
sont sur sa diagonale: 1 est l'unique valeur propre de 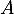 .
.
Si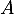 était diagonalisable, elle serait donc semblable à la matrice diagonale qui ne comporte que des 1 dans sa diagonale: l'identité
était diagonalisable, elle serait donc semblable à la matrice diagonale qui ne comporte que des 1 dans sa diagonale: l'identité 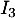 .
.
On aurait alors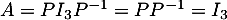 , ce qui n'est pas le cas.
Ainsi,
, ce qui n'est pas le cas.
Ainsi, 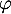 n'est pas diagonalisable.
n'est pas diagonalisable.
- D'après les calculs précédents, on a trouvé que
- On peut démontrer ce résultat par récurrence.
Cette expression est vraie pour
 , en prenant
, en prenant 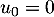 .
.
Puis, sin on suppose que cette expression de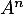 est vraie pour un certain entier
est vraie pour un certain entier 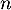 , alors le calcul de
, alors le calcul de 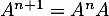 vérifie encore l'expression voulue, si tant est que
vérifie encore l'expression voulue, si tant est que
![\[u_{n+1}=u_n+\dfrac12n+\dfrac13\]](/Generateur-Devoirs/Colles/Applin/HEC-BL-2022-4.1_c/47.png)
Avec cette expression de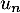 , le principe de récurrence montre alors que l'expression de
, le principe de récurrence montre alors que l'expression de 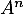 est vraie pour tout entier
est vraie pour tout entier 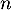 .
.
- On a trouvé que
![\[u_{k+1}-u_k=\dfrac12k+\dfrac13\]](/Generateur-Devoirs/Colles/Applin/HEC-BL-2022-4.1_c/51.png)
et donc, en sommant,
![\[\sum_{k=0}^{n-1}\left( u_{k+1}-u_k\rp=\sum_{k=0}^{n-1}\left(\dfrac12k+\dfrac13\rp\]](/Generateur-Devoirs/Colles/Applin/HEC-BL-2022-4.1_c/52.png)
La somme de gauche est télescopique, et on trouve donc
![\[u_n-u_0=\dfrac12\sum_{k=0}^{n-1}k+\dfrac13\sum_{k=0}^{n-1}1\]](/Generateur-Devoirs/Colles/Applin/HEC-BL-2022-4.1_c/53.png)
et donc, avec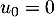 ,
,
![\[u_n=\dfrac12\,\dfrac{(n-1)n}2+\dfrac13n=\dfrac{n(3n+1)}{12}\]](/Generateur-Devoirs/Colles/Applin/HEC-BL-2022-4.1_c/55.png)
Tag:Applications linéaires
Autres sujets au hasard:

Voir aussi: