Projecteur composé de projecteurs
Colle de mathématiques
Sujet de colle de maths:- ProjecteursProjecteurs dans des espaces vectoriels
- Applications linéairesApplications linéaires
- Espace vectorielEspaces vectoriels
Énoncé du sujet
Soit  et
et  deux endomorphismes d'un espace vectoriel
deux endomorphismes d'un espace vectoriel  tels que
tels que
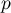 et
et  sont des projecteurs.
sont des projecteurs.
Montrer que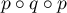 est aussi un projecteur.
est aussi un projecteur.
Montrer que
Correction
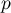 et
et 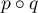 sont des projecteurs,
on a
sont des projecteurs,
on a  et
et 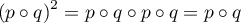
et alors
![\[\begin{array}{ll}
\left( p\circ q\circ p\rp^2
&=\left( p\circ q\circ p\rp\circ \left( p\circ q\circ p\rp\\[.7em]
&=p\circ q\circ p^2\circ q\circ p\\[.7em]
&=p\circ q\circ p\circ q\circ p\\[.7em]
&=\left( p\circ q\rp^2\circ p\\[.7em]
&=p\circ q\circ p
\enar\]](/Generateur-Devoirs/Colles/Applin/exP1_c/5.png)
et donc est bien un projecteur.
est bien un projecteur.
Correction
Commeet alors
![\[\begin{array}{ll}
\left( p\circ q\circ p\rp^2
&=\left( p\circ q\circ p\rp\circ \left( p\circ q\circ p\rp\\[.7em]
&=p\circ q\circ p^2\circ q\circ p\\[.7em]
&=p\circ q\circ p\circ q\circ p\\[.7em]
&=\left( p\circ q\rp^2\circ p\\[.7em]
&=p\circ q\circ p
\enar\]](/Generateur-Devoirs/Colles/Applin/exP1_c/5.png)
et donc
Tags:ProjecteursApplications linéairesEspace vectoriel
Autres sujets au hasard:

Voir aussi: