Endomorphisme de carré nul
Colle de mathématiques
Sujet de colle de maths:- Applications linéairesApplications linéaires
Énoncé du sujet
Soit  un endomorphisme non nul d'un
un endomorphisme non nul d'un 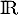 -espace vectoriel
-espace vectoriel 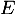 de dimension 3, tel que
de dimension 3, tel que 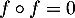 .
.
- Montrer que
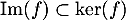 . Quel est le rang de
. Quel est le rang de 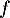 ?
?
- Montrer qu'il existe un vecteur
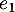 de
de 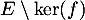 et un vecteur
et un vecteur 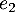 de
de 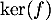 tels que
tels que  soit une base de
soit une base de 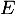 .
Écrire la matrice de
.
Écrire la matrice de 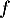 dans cette base.
dans cette base.
- Donner un exemple d'un tel endomorphisme dans
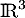 .
.
Correction
Correction
Oral ENSAE - 2017- Soit
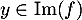 , alors il existe
, alors il existe 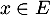 tel que
tel que
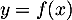 .
.
On a alors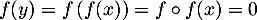 ,
ce qui signifie que
,
ce qui signifie que 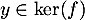 , et donc l'inclusion
, et donc l'inclusion
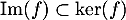 .
.
D'après le théorème du rang, on a
![\[\text{rg}(f)+\dim(\ker(f))=\dim(E)=3\]](/Generateur-Devoirs/Colles/Applin/carre-nul_c/7.png)
avec, d'après le résultat précédent,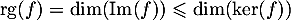 et on a donc
et on a donc
![\[3=\text{rg}(f)+\dim(\ker(f))\geqslant \text{rg}(f)+\text{rg}(f)\]](/Generateur-Devoirs/Colles/Applin/carre-nul_c/9.png)
d'où
![\[\text{rg}(f)\leqslant\dfrac32\]](/Generateur-Devoirs/Colles/Applin/carre-nul_c/10.png)
De plus, comme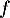 n'est pas l'application nulle, on a
n'est pas l'application nulle, on a
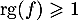 .
.
Finalement, on a trouvé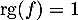 et alors
et alors
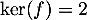 .
.
- On commence par construire une base du noyau, de dimension 2.
Soit
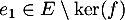 . On a alors
. On a alors 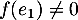 ,
et aussi
,
et aussi 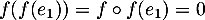 et donc
et donc 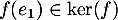 .
.
On complète ce vecteur par un vecteur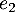 tel que
tel que
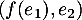 soit une base de
soit une base de 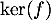 .
.
Il s'agit alors de montrer que la famille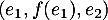 est une base
est une base 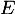 .
.
Il suffit de montrer que cette famille de 3 vecteurs dans un espace de dimension 3 est libre.
Soit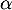 ,
, 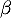 et
et 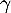 trois réels tels que
trois réels tels que
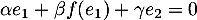 , alors, en appliquant
, alors, en appliquant 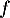 , on obtient aussi, puisque
, on obtient aussi, puisque 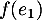 et
et 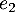 sont des éléments de
sont des éléments de 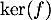 ,
,
![\[\alpha f(e_1)+\beta f\circ f(e_1)+\gamma f(e_2)=0
\iff\alpha f(e_1)=0\]](/Generateur-Devoirs/Colles/Applin/carre-nul_c/32.png)
d'où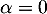 puisque aussi
puisque aussi 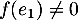 .
.
On a donc maintenant la relation
![\[\beta f(e_1)+\gamma e_2=0\]](/Generateur-Devoirs/Colles/Applin/carre-nul_c/35.png)
or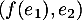 est une base de
est une base de 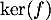 , en particulier la famille est libre, et la relation précédente implique donc que
, en particulier la famille est libre, et la relation précédente implique donc que 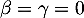 .
.
Finalement, on a bien montré que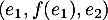 forme une base de
forme une base de 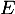 .
.
Dans cette base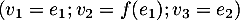 on a directement
on a directement 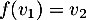 et
et 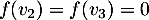 , d'où la matrice de
, d'où la matrice de 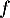 dans cette base
dans cette base
![\[\lp\begin{array}{ccc}
0&0&0\\
1&0&0\\
0&0&0\enar\rp\]](/Generateur-Devoirs/Colles/Applin/carre-nul_c/45.png)
- L'endomorphisme
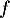 canoniquement associé à la matrice précédente est un exemple de tel endomorphisme: non nul et tel que
canoniquement associé à la matrice précédente est un exemple de tel endomorphisme: non nul et tel que 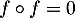 .
.
Tag:Applications linéaires
Autres sujets au hasard:
