Égalité des accroissements finis - Énoncé et démonstration
Colle de mathématiques
Sujet de colle de maths:- Rolle - AFThéorème de Rolle et théorème des accroissements finis
Énoncé du sujet
Énoncer l'égalité des accroissements finis.
Correction
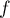 une fonction continue sur
une fonction continue sur ![$[a;b]$](/Generateur-Devoirs/Colles/Calcul/exAF0_c/2.png) et dérivable sur
et dérivable sur ![$]a;b[$](/Generateur-Devoirs/Colles/Calcul/exAF0_c/3.png) ,
alors il existe
,
alors il existe ![$c\in]a;b[$](/Generateur-Devoirs/Colles/Calcul/exAF0_c/4.png) tel que
tel que
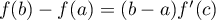 .
.
Démonstration:
Graphiquement, ce théorème énonce qu'il existe![$c\in]a;b[$](/Generateur-Devoirs/Colles/Calcul/exAF0_c/6.png) tel que
tel que
 ,
c'est-à-dire que la tangente est parallèle
à la droite passant par les points de la courbe aux extrémités
de l'intervalle:
,
c'est-à-dire que la tangente est parallèle
à la droite passant par les points de la courbe aux extrémités
de l'intervalle:
(.7,2)(2,3.5)(3.2,1)(4,1.5)(5,4)
\psline{<->}(.5,2.8)(3,4.2)
\psline{<->}(2.4,.4)(4.9,1.8)
\rput[r](-.2,1.5){$f(a)$}
\rput[r](-.2,4){$f(b)$}
\rput(.5,-.3){$a$}
\rput(5,-.3){$b$}
\psline[linestyle=dashed](.5,0)(.5,1.5)(0,1.5)
\psline[linestyle=dashed](5,0)(5,4)(0,4)
\psline(.5,1.5)(5,4)
\end{pspicture}\]](/Generateur-Devoirs/Colles/Calcul/exAF0_c/8.png)
Le coefficient directeur de la sécante pasant par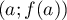 et
et 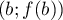 est
est  .
.
On définit alors la fonction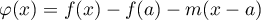 pour laquelle
pour laquelle
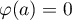 et aussi
et aussi  .
.
Comme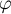 est, de même que
est, de même que 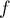 ,
continue sur
,
continue sur ![$[a;b]$](/Generateur-Devoirs/Colles/Calcul/exAF0_c/17.png) et dérivable sur
et dérivable sur ![$]a;b[$](/Generateur-Devoirs/Colles/Calcul/exAF0_c/18.png) ,
on en déduit, d'après le théorème de Rolle,
qu'il existe
,
on en déduit, d'après le théorème de Rolle,
qu'il existe ![$c\in]a;b[$](/Generateur-Devoirs/Colles/Calcul/exAF0_c/19.png) tel que
tel que
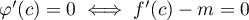 soit exactement
soit exactement
![\[f'(c)=m=\dfrac{f(b)-f(a)}{b-a}\]](/Generateur-Devoirs/Colles/Calcul/exAF0_c/21.png)
Correction
Théorème: SoitDémonstration:
Graphiquement, ce théorème énonce qu'il existe
(.7,2)(2,3.5)(3.2,1)(4,1.5)(5,4)
\psline{<->}(.5,2.8)(3,4.2)
\psline{<->}(2.4,.4)(4.9,1.8)
\rput[r](-.2,1.5){$f(a)$}
\rput[r](-.2,4){$f(b)$}
\rput(.5,-.3){$a$}
\rput(5,-.3){$b$}
\psline[linestyle=dashed](.5,0)(.5,1.5)(0,1.5)
\psline[linestyle=dashed](5,0)(5,4)(0,4)
\psline(.5,1.5)(5,4)
\end{pspicture}\]](/Generateur-Devoirs/Colles/Calcul/exAF0_c/8.png)
Le coefficient directeur de la sécante pasant par
On définit alors la fonction
Comme
Tag:Rolle - AF
Autres sujets au hasard:

Voir aussi: