Variante du théorème des accroissements finis
Colle de mathématiques
Sujet de colle de maths:- Rolle - AFThéorème de Rolle et théorème des accroissements finis
Énoncé du sujet
Soit  une fonction définie et continue sur
une fonction définie et continue sur
![$[a,b]$](/Generateur-Devoirs/Colles/Calcul/exAF0.2/2.png) ,
dérivable sur
,
dérivable sur ![$]a;b[$](/Generateur-Devoirs/Colles/Calcul/exAF0.2/3.png) , telle que
, telle que  ,
et soit
,
et soit 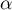 à l'extérieur de
à l'extérieur de ![$[a;b]$](/Generateur-Devoirs/Colles/Calcul/exAF0.2/6.png) .
.
En introduisant la fonction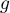 définie sur
définie sur ![$[a;b]$](/Generateur-Devoirs/Colles/Calcul/exAF0.2/8.png) par
par
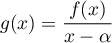 ,
montrer qu'il existe
,
montrer qu'il existe 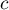 dans
dans ![$]a;b[$](/Generateur-Devoirs/Colles/Calcul/exAF0.2/11.png) tel que
tel que
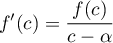 .
.
Donner une interprétation géométrique de la fonction et énoncer le résultat obtenu sous forme géométrique.
et énoncer le résultat obtenu sous forme géométrique.
En introduisant la fonction
Donner une interprétation géométrique de la fonction
Correction
 est, comme
est, comme 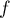 , continue sur
, continue sur ![$[a;b]$](/Generateur-Devoirs/Colles/Calcul/exAF0.2_c/3.png) et dérivable sur
et dérivable sur ![$]a;b[$](/Generateur-Devoirs/Colles/Calcul/exAF0.2_c/4.png) ,
avec, comme pour
,
avec, comme pour 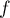 aussi,
aussi,
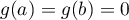 .
.
Ainsi, d'après le théorème de Rolle, il existe![$c\in]a;b[$](/Generateur-Devoirs/Colles/Calcul/exAF0.2_c/7.png) tel que
tel que
![\[g'(c)=\dfrac{f'(x)}{c-\alpha}-\dfrac{f(c)}{(c-\alpha)^2}=0\]](/Generateur-Devoirs/Colles/Calcul/exAF0.2_c/8.png)
soit exactement,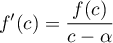 .
.
Graphiquement,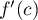 est le coefficient directeur de la tangente
à la courbe de
est le coefficient directeur de la tangente
à la courbe de 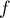 au point d'abscisse
au point d'abscisse 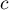 ,
tandis que
,
tandis que
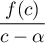 est le coefficient directeur
de la droite passant par
est le coefficient directeur
de la droite passant par 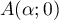 et
et 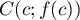 .
.
Graphiquement, on peut tracer une tangente à la courbe de en partant
du point
en partant
du point 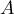 .
.
(3.3,3.56)\rput(3.3,-.3){$c$}
\rput(3.2,3.7){$C$}
\end{pspicture}\]](/Generateur-Devoirs/Colles/Calcul/exAF0.2_c/18.png)
Correction
Ainsi, d'après le théorème de Rolle, il existe
soit exactement,
Graphiquement,
Graphiquement, on peut tracer une tangente à la courbe de
(3.3,3.56)\rput(3.3,-.3){$c$}
\rput(3.2,3.7){$C$}
\end{pspicture}\]](/Generateur-Devoirs/Colles/Calcul/exAF0.2_c/18.png)
Tag:Rolle - AF
Autres sujets au hasard:

Voir aussi: