Encadrement accroissements finis et convergence d'une somme partielle


Colle de mathématiques

Sujet de colle de maths:
  • Rolle - AFThéorème de Rolle et théorème des accroissements finis
  • SommesSommes des termes d'une suite

Énoncé du sujet

  1. Montrer que, pour tout entier naturel, on a
    \[\dfrac{1}{(n+1)^2+1}\leqslant\arctan(n+1)-\arctan(n)\leqslant\dfrac{1}{n^2+1}\]

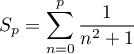
  2. En déduire un encadrement de la somme $S_p=\dsp\sum_{n=0}^p\dfrac{1}{n^2+1}$
  3. Montrer que la suite $\left( S_p\rp$ est convergente et déterminer sa limite.



Correction

Correction

  1. En appliquant le théorème des accroissements finis à la fonction 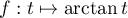$f:t\mapsto\arctan t$ sur l'intervalle $[n,n+1]$, il existe $c$ dans $]n,n+1[$ tel que
    \[f(n+1)-f(n)=(n+1-n)f'(c)=\dfrac{1}{1+c^2}\]

    soit alors, comme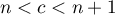 $n<c<n+1$
    \[\dfrac{1}{(n+1)^2+1}<\arctan(n+1)-\arctan(n)=\dfrac{1}{1+c^2}<\dfrac{1}{n^2+1}\]


  2. On a donc d'une part que
    \[\arctan(n+1)-\arctan(n)<\dfrac{1}{n^2+1}\]

    et donc, en sommant de $n=0$ à $n=p$,
    \[\sum_{n=0}^p \lp\arctan(n+1)-\arctan(n)\right) =\arctan(p)<S_p\]


    D'autre part, en remplaçant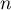 $n$ par $n-1$ dans l'inégalité de gauche de la question précédente,
    \[\dfrac{1}{n^2+1}<\arctan(n)-\arctan(n-1)\]

    et en sommant de $n=1$ à $p$,
    \[S_p-1<\arctan(p+1)\]


    En résumé, on a obtenu l'encadrement
    \[\arctan(p)<S_p<1+\arctan(p)\]


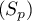  3. La suite $\left( S_p\rp$ est bornée d'après ce qui précède, comme $-\pi/2<\arctan(x)<\pi/2$:
    \[-\dfrac\pi2<S_p<\dfrac\pi2+1\]

    On pense donc à étudier son sens de variation:
    \[S_{p+1}-S_p=\dfrac{1}{(p+1)^2+1}>0\]

    ce qui montre que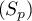 $\left( S_p\rp$ est strictement croissante.
    Comme elle est de plus bornée, donc majorée, elle est convergente vers une limite $l\in\R$.

    Enfin, en passant à la lmite dans l'encadrement de $S_p$, on peut dire que
    \[\dfrac\pi2\leqslant l\leqslant1+\dfrac\pi2\]



Tags:Rolle - AFSommes

Autres sujets au hasard: Lancer de dés

Voir aussi:
LongPage: h2: 3 - h3: 0