Égalité d'un polynôme et de l'exponentielle: finitude des solutions
Colle de mathématiques
Sujet de colle de maths:- DérivéeEtude de fonctions (dérivée, continuité, variations, limites, ...)
- Rolle - AFThéorème de Rolle et théorème des accroissements finis
Énoncé du sujet
Soit 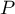 un polynôme.
Montrer que l'équation
un polynôme.
Montrer que l'équation 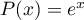 n'admet qu'un nombre fini de solutions.
n'admet qu'un nombre fini de solutions.
Correction
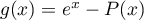 .
Si
.
Si 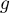 admet
admet 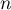 racines,
alors
racines,
alors 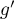 en admet
en admet  , d'après le théorème de Rolle.
En réappliquant ce théorème à
, d'après le théorème de Rolle.
En réappliquant ce théorème à 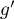 , on obtient que
, on obtient que 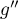 admet
admet
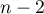 racines, et en réitérant,
racines, et en réitérant,
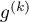 admet
admet 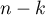 racines, et enfin
racines, et enfin 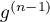 admet 1 racine.
admet 1 racine.
Ainsi, si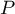 est un polynôme de degré
est un polynôme de degré 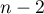 , alors
, alors 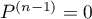 et donc
et donc 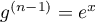 devrait admettre 1 racine, ce qui est absurde.
devrait admettre 1 racine, ce qui est absurde.
Ainsi,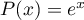 ne peut pas admettre plus de
ne peut pas admettre plus de  racines où
racines où
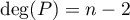 .
.
Correction
SoitAinsi, si
Ainsi,
Tags:DérivéeRolle - AF
Autres sujets au hasard:

Voir aussi: