Deux tentatives pour joindre des correspondants
Colle de mathématiques
Sujet de colle de maths:- Couples de variables aléatoiresCouples de variables aléatoires
Énoncé du sujet
Une secrétaire cherche à joindre 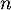 correspondants.
Pour chaque appel, indépendamment, elle a une probabilité
correspondants.
Pour chaque appel, indépendamment, elle a une probabilité 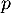 de les joindre, avec
de les joindre, avec ![$p\in]0, 1[$](/Generateur-Devoirs/Colles/CVA/secretaire-correspondants/3.png) .
.
Soit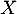 la variable aléatoire qui compte le nombre de correspondants qu'elle parvient à joindre dès la première tentative.
la variable aléatoire qui compte le nombre de correspondants qu'elle parvient à joindre dès la première tentative.
Soit
- Donner la loi de
 , son espérance et sa variance.
, son espérance et sa variance.
- Soit
 la variable qui compte le nombre de correspondants qu'elle parvient à joindre lors d'une seconde tentative (elle contacte
la variable qui compte le nombre de correspondants qu'elle parvient à joindre lors d'une seconde tentative (elle contacte  personnes).
personnes).
Soit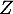 la variable aléatoire donnée par
la variable aléatoire donnée par 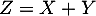 .
Donner le support de
.
Donner le support de 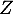 .
.
- Calculer
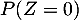 et
et 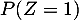 .
.
- Donner la loi de
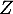 .
.
Correction
Correction
Oral ENSAE - Saclay - 2019- On répète
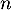 fois l'expérience aléatoire "appeler un corresponnant",
de manière identique et indépendante, et dont le succès est "le correspondant répond" de probabilité
fois l'expérience aléatoire "appeler un corresponnant",
de manière identique et indépendante, et dont le succès est "le correspondant répond" de probabilité  .
.
La variable aléatoire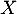 , qui est égale au nombre succès, suit donc la loi binomiale de paramètres
, qui est égale au nombre succès, suit donc la loi binomiale de paramètres 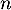 et
et 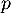 .
Son espérance est
.
Son espérance est 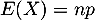 et sa variance
et sa variance 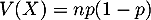 .
.
-
![$Z(\Omega)=[\![0; n ]\!]$](/Generateur-Devoirs/Colles/CVA/secretaire-correspondants_c/8.png) , car
, car 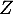 compte le nombre de correspondants qu'elle parvient à joindre au total, 1er et 2ème appel.
compte le nombre de correspondants qu'elle parvient à joindre au total, 1er et 2ème appel.
-
![\[\begin{array}{ll}P(Z = 0)&=P\left( X=0\cap Y=0\rp\\
&=(1-p)^n(1-p)^n\\
&=(1-p)^{2n}\enar\]](/Generateur-Devoirs/Colles/CVA/secretaire-correspondants_c/10.png)
et
![\[\begin{array}{lcl}P(Z = 1)&=&P\left( X=0\cap Y=1\rp+P\left( X=1\cap Y=0\rp\\
&=&(1-p)^n\times np(1-p)^{n-1}
+np(1-p)^{n-1}\times (1-p)^{n-1}\\
&=&np(1-p)^{2n-2}\left( (1-p)+1\rp\\
&=&np(1-p)^{2n-2}\left( 2-p\rp\\
\enar\]](/Generateur-Devoirs/Colles/CVA/secretaire-correspondants_c/11.png)
- D'après la formule des probabilités totales, et en posant
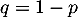 ,
,
![\[\begin{array}{lcl}
P(Z=k)&=&\dsp\sum_{i=0}^kP(X=i\cap Y=k-i)\\
&=&\dsp\sum_{i=0}^kP(X=i)\,P\left( Y=k-i| X=i\rp\\
&=&\dsp\sum_{i=0}^k\binom{n}{i}p^iq^{n-i}\binom{n-i}{k-i}p^{k-i}q^{(n-i)-(k-i)}\\
&=&p^kq^{2n-k}\dsp\sum_{i=0}^k\binom{n}{i}\binom{n-i}{k-i}q^{-i}
\enar\]](/Generateur-Devoirs/Colles/CVA/secretaire-correspondants_c/13.png)
où
![\[\begin{array}{lcl}\dsp\binom{n}{i}\binom{n-i}{k-i}
&=&\dfrac{n!}{i!(n-i)!}\tm\dfrac{(n-i)!}{(k-i)!(n-k)!}\\
&=&\dfrac{n!}{i!(k-i)!(n-k)!}\\
&=&\dfrac{n!}{k!(n-k)!}\dsp\binom{k}{i}\\
&=&\dsp\binom{n}{k}\binom{k}{i}\\
\enar\]](/Generateur-Devoirs/Colles/CVA/secretaire-correspondants_c/14.png)
d'où
![\[\begin{array}{lcl}P(Z=k)
&=&\dsp\binom{n}{k}p^kq^{2n-k}\sum_{i=0}^k\binom{k}{i}\lp\dfrac1q\rp^i
\enar\]](/Generateur-Devoirs/Colles/CVA/secretaire-correspondants_c/15.png)
soit, avec la formule du biôme de Newton:
![\[\begin{array}{lcl}P(Z=k)
&=&\dsp\binom{n}{k}p^kq^{2n-k}\lp1+\dfrac1q\rp^k\\
&=&\dsp\binom{n}{k}\left( q^2\rp^{n-k}\left( p(1+q)\rp^k\\
\enar\]](/Generateur-Devoirs/Colles/CVA/secretaire-correspondants_c/16.png)
or
![\[p(1+q)=(1-q)(1+q)=1-q^2\]](/Generateur-Devoirs/Colles/CVA/secretaire-correspondants_c/17.png)
d'où
![\[P(Z=k)=\dsp\binom{n}{k}\left( q^2\rp^{n-k}\left(1-q^2\rp^k\]](/Generateur-Devoirs/Colles/CVA/secretaire-correspondants_c/18.png)
ce qui montre que, finalement, la variable aléatoire suit la loi binomiale de paramètres
suit la loi binomiale de paramètres 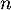 et
et
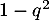 .
.
Tag:Couples de variables aléatoires
Autres sujets au hasard:

Voir aussi: