Covariance d'une loi normale et de son carré
Colle de mathématiques
Sujet de colle de maths:- Couples de variables aléatoiresCouples de variables aléatoires
Énoncé du sujet
On considère une variable aléatoire 
qui suit la loi normale centrée réduite, et on définit la variable aléatoire 
par 
.
Calculer la covariance de
et 
.
Les variables
et 
sont-elles indépendantes ?
qui suit la loi normale centrée réduite, et on définit la variable aléatoire 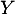par .
Calculer la covariance de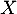
et .
Les variables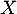
et sont-elles indépendantes ?
Correction
![\[cov(X,Y)=E(XY)-E(X)E(Y)\]](/Generateur-Devoirs/Colles/CVA/covariance-2_c/1.png)
avec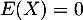
puisque 
ewt centrée.
De plus,
![\[E(XY)=E(X^3)=\int_\R x^3f(x)dx\]](/Generateur-Devoirs/Colles/CVA/covariance-2_c/4.png)
où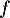
est la densité de la loi normale centrée réduite.
Comme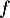 
est paire, on a 
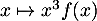impaire, et donc l'intégrale est nulle.
On en déduit que la covariance est nulle.
Attention, on ne peut pas en déduire pour autant que ces variables sont indépendantes.
Au contraire même ces variables semblent plutôt clairement dépendantes,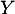
étant définie à partir de 
.
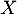Correction
On aavec
puisque ewt centrée.
De plus,
où
est la densité de la loi normale centrée réduite.
Comme est paire, on a impaire, et donc l'intégrale est nulle.
On en déduit que la covariance est nulle.
Attention, on ne peut pas en déduire pour autant que ces variables sont indépendantes.
Au contraire même ces variables semblent plutôt clairement dépendantes,
étant définie à partir de .
Tag:Couples de variables aléatoires
Autres sujets au hasard:
Voir aussi: