Convergence d'une suite définie par un encadrement


Colle de mathématiques

Sujet de colle de maths:

Énoncé du sujet

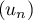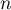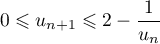Soit $(u_n)$ une suite telle que, pour tout entier $n$, $0\leqslant u_{n+1}\leqslant 2-\dfrac{1}{u_n}$.
Étudier la convergence d'une telle suite.


Correction

Correction

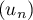$\left( u_n\rp$ est minorée (par $0$).
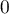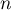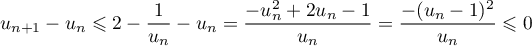
De plus, pour tout $n$, $u_{n+1}-u_n\leqslant 2-\dfrac{1}{u_n}-u_n =\dfrac{-u_n^2+2u_n-1}{u_n} =\dfrac{-(u_n-1)^2}{u_n}\leqslant0$
et ainsi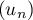 $\left( u_n\rp$ est décroissante.
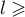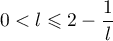Comme elle est de plus minorée, on en déduit qu'elle converge vers une limite $l\geqslant$ telle que $0<l\leqslant2-\dfrac1l$.
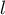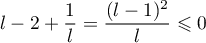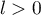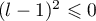Ainsi, $l$ vérifie $l-2+\dfrac1l=\dfrac{(l-1)^2}{l}\leqslant0$, d'où, comme $l>0$, $(l-1)^2\leqslant0$ et donc nécessairement $l=1$.
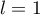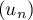$\left( u_n\rp$ est donc une suite décroissante convergeant vers 1.


Tags:SuitesLimite

Autres sujets au hasard: Lancer de dés

Voir aussi:
LongPage: h2: 3 - h3: 0