Décomposition harmonique d'un signal triangulaire

Colle de mathématiques

Sujet de colle de maths:

Série de FourierSérie de Fourier

Énoncé du sujet

Soit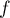

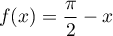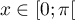la fonction 2 $\pi$ -périodique et paire définie par, $f(x)=\dfrac\pi2-x$ pour tout $x\in[0;\pi[$ .

Déterminer la série de Fourier de .
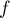En déduire la somme 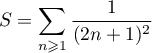$S=\dsp\sum_{n\geqslant1}\dfrac1{(2n+1)^2}$ puis la somme $T=\dsp\sum_{n\geqslant1}\dfrac1{n^2}$ .

Correction

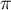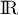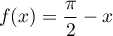- La fonction est 2 $\pi$ -périodique, continue sur $\R$ et affine par morceaux avec, pour tout $x\in[0;\pi]$ , $f(x)=\dfrac\pi2-x$ .
  La fonction est paire et donc, pour tout entier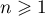 $n\geqslant1$ ,
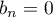
- sa valeur moyenne est aussi nulle:
  
  $\begin{array}{ll}a_0&\dsp=\dfrac{1}{2\pi}\int_{-\pi}^\pi f(t)\,dt \\[1.2em] &\dsp=\dfrac1\pi\int_0^\pi f(t)\,dt\\[1.2em] &\dsp=\dfrac1\pi\int_0^\pi\lp\dfrac\pi2-t\rp\,dt\\[1.2em] &\dsp=\dfrac1\pi\Bigl[\,\dfrac\pi2t-\dfrac{t^2}{2}\,\Bigr]_0^\pi\\[1em] &=0 \enar$
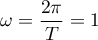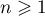- La pulsation est $\omega=\dfrac{2\pi}{T}=1$ et alors, pour tout entier $n\geqslant1$ , on a
  
  $\begin{array}{ll} a_n&=\dsp\dfrac4T\int_0^\pi f(t)\cos(n\omega t)\,dt\\[1.2em] &=\dsp\dfrac2\pi\int_0^\pi\lp\dfrac\pi2-t\rp\cos(nt)dt \enar$
  
  soit, en intégrant par parties,
  
  $a_n=\dfrac2\pi\Bigr[\lp\dfrac\pi2-t\rp\dfrac{\sin(nt)}{n}\Bigr]_0^\pi -\dfrac2\pi\int_0^\pi(-1)\dfrac{sin(nt)}{n}dt$
  
  et donc, puisque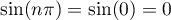 $\sin(n\pi)=\sin(0)=0$ ,
  
  $\begin{array}{ll}a_n&\dsp=\dfrac2{n\pi}\int_0^\pi\sin(nt)dt\\[1.2em] &\dsp=\dfrac2{n\pi}\Bigl[-\dfrac{\cos(nt)}{n}\Bigr]_0^\pi \enar$
  
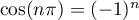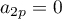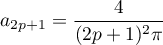
  enfin, comme $\cos(n\pi)=(-1)^n$ , on obtient donc que les coefficients de rang pair sont nuls: $a_{2p}=0$ et ceux de rang impair valent $a_{2p+1}=\dfrac4{(2p+1)^2\pi}$
- Comme 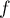est continue sur 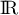$\R$ , on obtient pour tout 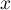réel,
  
  $f(x)=\dfrac4\pi\sum_{p\geqslant1}\dfrac{\cos\bigl((2p+1)x\bigr)}{(2p+1)^2}$
On en déduit en particulier, pour , que

$f(0)=\dfrac\pi2=\dfrac4\pi\sum_{p\geqslant1}\dfrac1{(2p+1)^2}$

d'où

$S=\dsp\sum_{n\geqslant1}\dfrac1{(2n+1)^2}=\dfrac{\pi^2}{8}$

et alors, pour la somme de Riemann, en décomposant termes pairs/impairs,

$\begin{array}{ll}T&=\dsp\sum_{n\geqslant1}\dfrac1{n^2}\\[1em] &=\dsp\sum_{n\geqslant1}\dfrac1{(2n)^2} +\sum_{n\geqslant1}\dfrac1{(2n+1)^2}\\[1em] &=\dsp\dfrac14T+S \enar$

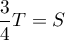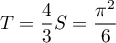On trouve donc $\dfrac34T=S$ , soit $T=\dfrac43S=\dfrac{\pi^2}{6}$ .

Tag:Série de Fourier

Autres sujets au hasard:

Voir aussi: