Suite, équivalents et série
Colle de mathématiques
Sujet de colle de maths:Énoncé du sujet
On considère la fonction 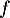 donnée par:
donnée par:
![\[f(x)=\dfrac{1-cos(x)}{x}\]](/Generateur-Devoirs/Colles/Suites/suiteeqserie/2.png)
et la suite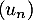 définie par
définie par ![$u_0\in\left]0,\dfrac\pi2\right]$](/Generateur-Devoirs/Colles/Suites/suiteeqserie/4.png) et
et 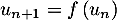 pour tout
pour tout 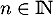 .
.
et la suite
- Montrer que
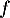 se prolonge en une fonction continue sur
se prolonge en une fonction continue sur 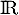 .
.
- Montrer que pour tout
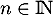 ,
, ![$u_n\in]0, 1]$](/Generateur-Devoirs/Colles/Suites/suiteeqserie/10.png) .
.
- Montrer que
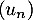 est décroissante, convergente et calculer sa limite.
est décroissante, convergente et calculer sa limite.
- Montrer que
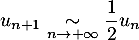 .
.
La série de terme général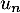 converge-t-elle ?
converge-t-elle ?
- Pour quelles valeurs de a la série de terme général
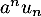 converge-t-elle ?
converge-t-elle ?
Correction
On considère la fonction donnée par:
donnée par:
![\[f(x)=\dfrac{1-cos(x)}{x}\]](/Generateur-Devoirs/Colles/Suites/suiteeqserie_c/2.png)
et la suite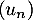 définie par
définie par ![$u_0\in\left]0,\dfrac\pi2\right]$](/Generateur-Devoirs/Colles/Suites/suiteeqserie_c/4.png) et
et 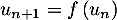 pour tout
pour tout 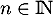 .
.
Correction
Oral ENSAE - Saclay - 2019On considère la fonction
et la suite
-
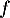 est clairement continue sur
est clairement continue sur 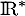 comme quotient de fonctions continues sur
comme quotient de fonctions continues sur 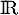 et dont le déniminateur ne s'annule qu'en 0.
et dont le déniminateur ne s'annule qu'en 0.
En 0, on a
![\[\cos(x)=1-\dfrac{x^2}2+o\left( x^2\rp\]](/Generateur-Devoirs/Colles/Suites/suiteeqserie_c/10.png)
et donc
![\[1-\cos(x)\underset{0}{\sim}\dfrac{x^2}2\]](/Generateur-Devoirs/Colles/Suites/suiteeqserie_c/11.png)
et alors, par quotient,
![\[f(x)\underset{0}{\sim}\dfrac{x}2\]](/Generateur-Devoirs/Colles/Suites/suiteeqserie_c/12.png)
ce qui montre que
![\[\lim_{x\to0}f(x)=0\]](/Generateur-Devoirs/Colles/Suites/suiteeqserie_c/13.png)
Ainsi, on peut prolonger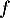 en
en 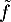 par continuité en 0,
en posant
par continuité en 0,
en posant 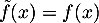 pour
pour 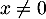 et
et 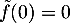 .
.
- On peut étudier les variations de
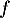 , qui est bien dérivable sur
, qui est bien dérivable sur 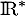 donc sur
donc sur ![$\left]0,\dfrac\pi2\right]$](/Generateur-Devoirs/Colles/Suites/suiteeqserie_c/21.png) , avec
, avec
![\[f'(x)=\dfrac{x\sin(x)-1+\cos(x)}{x^2}\]](/Generateur-Devoirs/Colles/Suites/suiteeqserie_c/22.png)
Le signe du numérateur est problématique; on peut l'étudier à part: soit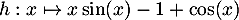 .
.
Alors,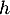 est dérivable sur
est dérivable sur 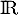 avec
avec
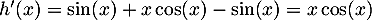 et on a donc
et on a donc 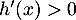 pour tout
pour tout ![$x\in\left]0,\dfrac\pi2\right[$](/Generateur-Devoirs/Colles/Suites/suiteeqserie_c/28.png) .
.
Ainsi,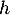 est strictement croissante et donc
pour
est strictement croissante et donc
pour 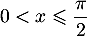 on a en particulier
on a en particulier 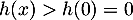 et donc
et donc 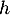 , comme
, comme 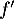 , est strictement positive et la fonction
, est strictement positive et la fonction 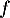 est donc strictement croissante.
est donc strictement croissante.
Maintenant, on a![$u_0\in\left]0,\dfrac\pi2\right]\iff 0<u_0\leqslant\dfrac\pi2$](/Generateur-Devoirs/Colles/Suites/suiteeqserie_c/35.png) ,
et donc, comme
,
et donc, comme 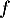 strictement croissante,
strictement croissante,
![\[\lim_{x\to0}f(x)=0< f(u_0)=u_1\leqslant f\lp\dfrac\pi2\rp=\dfrac2\pi\leqslant1\]](/Generateur-Devoirs/Colles/Suites/suiteeqserie_c/37.png)
puis, en réitérant ce raisonnement, par récurrence, si![$u_n\in]0;1]$](/Generateur-Devoirs/Colles/Suites/suiteeqserie_c/38.png) ,
alors
,
alors
![\[0<u_{n+1}=f(u_n)\leqslant f(1)<f\lp\dfrac\pi2\rp<1\]](/Generateur-Devoirs/Colles/Suites/suiteeqserie_c/39.png)
ce qui montre bien que![$u_n\in]0;1]$](/Generateur-Devoirs/Colles/Suites/suiteeqserie_c/40.png) pour tout entier
pour tout entier 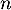 .
.
- Pour étudier le sens de variation de
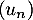 on peut érudier le signe de
on peut érudier le signe de
![\[f(x)-x=\dfrac{1-\cos(x)-x^2}{x}\]](/Generateur-Devoirs/Colles/Suites/suiteeqserie_c/43.png)
Comme ici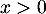 , le signe de
, le signe de 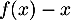 est celui de
est celui de 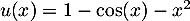 .
.
On a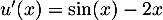 , que l'on peut à nouveau dériver:
, que l'on peut à nouveau dériver:
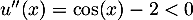 , donc
, donc
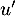 est strictement décroissante, donc
est strictement décroissante, donc
![\[x\in\left]0;\dfrac\pi2\right]\iff u'(0)=0>u'(x)\geqslant u'\lp\dfrac\pi2\rp=1-\pi\]](/Generateur-Devoirs/Colles/Suites/suiteeqserie_c/50.png)
Ainsi, en particulier,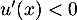 et donc
et donc 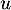 est strictement décroissante,
et donc
est strictement décroissante,
et donc
![\[x\in\left]0;\dfrac\pi2\right]\iff u(0)=0>u(x)\geqslant u\lp\dfrac\pi2\rp\]](/Generateur-Devoirs/Colles/Suites/suiteeqserie_c/53.png)
et en particulier,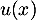 , comme
, comme 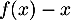 est négatif.
est négatif.
Ainsi, comme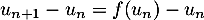 , la suite
, la suite
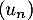 est aussi décroissante.
est aussi décroissante.
Comme cette suite est de plus minorée par 0, on en déduit qu'elle converge vers une limite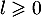 , telle que
, telle que
![\[\tilde{f}(l)=l\]](/Generateur-Devoirs/Colles/Suites/suiteeqserie_c/59.png)
soit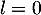 , le seul point fixe de
, le seul point fixe de 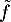 .
.
- Comme
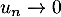 , on a l'équivalent
, on a l'équivalent
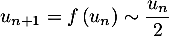 .
.
En particulier, on a
![\[\lim_{n\to+\infty}\dfrac{u_{n+1}}{u_n}=\dfrac12<1\]](/Generateur-Devoirs/Colles/Suites/suiteeqserie_c/64.png)
ce qui montre, d'après le critère de D'Alembert, que la série de terme général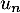 est convergente.
est convergente.
- Soit
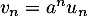 , alors
, alors
![\[\dfrac{v_{n+1}}{v_n}=a\dfrac{u_{n+1}}{u_n}\]](/Generateur-Devoirs/Colles/Suites/suiteeqserie_c/67.png)
et donc
![\[\lim_{n\to+\infty}\dfrac{v_{n+1}}{v_n}=\dfrac{a}2\]](/Generateur-Devoirs/Colles/Suites/suiteeqserie_c/68.png)
D'après le critère de D'Alembert, la série de terme général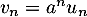 converge lorsque
converge lorsque 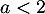 et diverge lorsque
et diverge lorsque 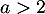 , tandis qu'on ne peut pas conclure ainsi pour
, tandis qu'on ne peut pas conclure ainsi pour  .
.
Tags:SuitesSéries
Autres sujets au hasard:

Voir aussi: