Convergence de la série exponentielle (avec une récurrence)


Colle de mathématiques

Sujet de colle de maths:

Énoncé du sujet

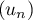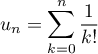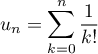Soit la suite $(u_n)$ définie par $u_n=\dsp\sum_{k=0}^n \dfrac1{k!}$.
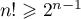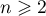  1. Montrer que $n!\geqslant 2^{n-1}$ pour $n\geqslant2$.
    En déduire que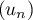 $(u_n)$ est majorée par 3.
  2. Montrer que $(u_n)$ converge.



Correction

Correction

  1. On peut démontrer cette propriété par récurrence.
    Pour $n=2$, $2!=2$ et $2^{2-1}=2$, et la propriété est donc vraie initialement.

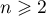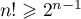    Supposons que la propriété soit vraie à un certain rang $n\geqslant2$, c'est-à-dire que $n!\geqslant2^{n-1}$.
    On a alors, au rang suivant, $(n+1)!=n!(n+1)\geqslant 2^{n-1}(n+1)$.
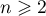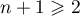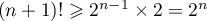    Or, pour $n\geqslant2$, $n+1\geqslant2$, et donc, $(n+1)!\geqslant 2^{n-1}\tm2=2^n$.
    La propriété est ainsi encore vraie au rang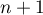 $n+1$.

    D'après le principe de récurrence, la propriété est donc vraie pour tout entier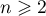 $n\geqslant2$.

    On a alors,
    \[\begin{array}{ll} u_n&\dsp=\dsp\sum_{k=0}^n\dfrac{1}{k!} =1+1+\sum_{k=2}^n\dfrac{1}{k!} \\[1em] &\dsp\leqslant2+\sum_{k=2}^n\dfrac{1}{2^{k-1}} =2+\dfrac12\dfrac{1-\lp\dfrac12\rp^{n-1}}{1-\dfrac12}\\[1em] &\dsp=2+1-\lp\dfrac12\rp^{n-1} =3-\lp\dfrac12\rp^{n-1}\leqslant3 \enar\]

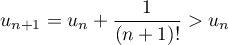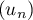  2. Enfin, comme $u_{n+1}=u_n+\dfrac{1}{(n+1)!}>u_n$, donc que la suite $\left( u_n\rp$ est (strictement) croissante, et majorée d'après la question précédente, on en déduit qu'elle est convergente vers un réle $l\leqslant3$.


Tags:SuitesRécurrenceSommesLimite

Autres sujets au hasard: Lancer de dés

Voir aussi:
LongPage: h2: 3 - h3: 0