Suite récurrente définie par une fonction - Inégalité des accroissements finis
Colle de mathématiques
Sujet de colle de maths:Énoncé du sujet
On considère la suite 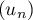 définie par
définie par 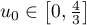 et
et 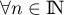 ,
, 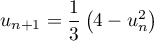 .
.
Justifier que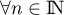 ,
, 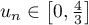 .
.
A l'aide de l'inégalité des accroissements finis, montrer que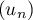 converge vers 1.
converge vers 1.
Justifier que
A l'aide de l'inégalité des accroissements finis, montrer que
Correction
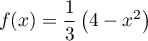 et
et 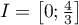 , de telle que sorte que
, de telle que sorte que
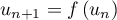 .
.
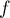 est dérivable sur
est dérivable sur 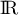 avec
avec 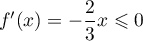 sur
sur 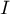 .
Ainsi
.
Ainsi 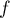 est décroissante sur
est décroissante sur 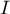 ,
et comme
,
et comme 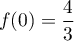 et
et 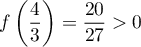 on a
on a 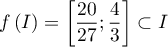 ,
et
,
et 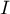 est donc stable par
est donc stable par 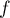 .
.
Ainsi, si ,
, 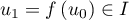 ,
puis par une récurrence immédiate, pour tout entier
,
puis par une récurrence immédiate, pour tout entier 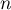 ,
,
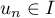 .
.
On veut montrer la convergence de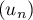 vers 1, donc majorer
vers 1, donc majorer
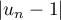 , ou encore, comme
, ou encore, comme 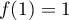 ,
,
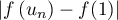 ,
d'où l'idée d'utiliser l'inégalité des accroissements finis sur l'intervalle
,
d'où l'idée d'utiliser l'inégalité des accroissements finis sur l'intervalle
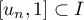 ou
ou 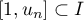 .
.
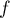 est continue et dérivable sur
est continue et dérivable sur 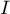 , et
pour tout
, et
pour tout 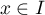 , on a
, on a 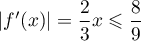 .
.
L'inégalité des accroissements finis avec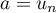 et
et 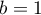 donne alors
donne alors
![\[\left|f\left( u_n\right) -f(1)\right|=\left|u_{n+1}-1\right|\leqslant\dfrac89\left|u_n-1\right|\]](/Generateur-Devoirs/Colles/Calcul/exIAsuite1_c/31.png)
Par une récurrence immédiate, on trouve alors
![\[\left|u_n-1\left|\leqslant\lp\dfrac89\rp^n\left|u_0-1\right|\]](/Generateur-Devoirs/Colles/Calcul/exIAsuite1_c/32.png)
et comme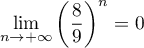 ,
on en déduit que
,
on en déduit que 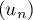 converge bien vers 1.
converge bien vers 1.
Correction
SoitAinsi, si
On veut montrer la convergence de
L'inégalité des accroissements finis avec
Par une récurrence immédiate, on trouve alors
et comme
Tags:SuitesDérivée
Autres sujets au hasard:

Voir aussi: