Choix aléatoire de pâtes dans un restaurant italien
Colle de mathématiques
Sujet de colle de maths:- Probabilités conditionnelles - indépendanceProbabilités conditionnelles - indépendance
Énoncé du sujet
Une personne se rend chaque semaine dans un restaurant italien pour déguster des pâtes, et choisit entre trois recettes classiques:
Arrabiata (notée A), Bolognaise (notée B) et Carbonara (notée C).
La première semaine, elle choisit les pâtes bolognaise.
Après avoir dégusté des pâtes bolognaise, la semaine suivante la personne choisit les pâtes bolognaise avec probabilité 2/3 et les pâtes carbonara avec probabilité 1/3.
Après avoir dégusté les pâtes carbonara, la semaine suivante la personne choisit les pâtes carbonara avec probabilité 1/3 et les pâtes à l'arrabiata avec probabilité 2/3. Enfin, après avoir dégusté les pâtes à l'arrabiata, la personne choisit ces mâme pâtes la semaine suivante.
On note 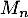 la variable aléatoire à valeurs dans
la variable aléatoire à valeurs dans 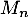 qui donne le menu choisi la semaine
qui donne le menu choisi la semaine 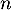 .
.
- Donner la valeur de
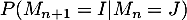 pour tous
pour tous 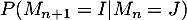 .
.
Dans la suite de l'exercice, on note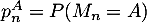 ,
,
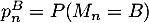 et
et 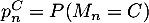 .
.
- Exprimer
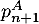 ,
, 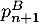 et
et 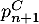 en fonction de
en fonction de
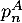 ,
, 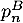 et
et 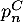 .
.
- Exprimer
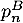 en fonction de
en fonction de 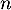 .
.
- Soit
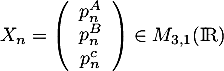 .
Montrer que
.
Montrer que 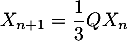 avec
avec 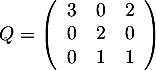 .
.
- Calculer les valeurs propres de la matrice
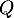 .
.
- Montrer que
![\[X_n=P\lp\begin{array}{ccc}1&0&0\\
0&\lp\dfrac23\rp^{n-1}&0\\
0&0&\lp\dfrac13\rp^{n-1}
\enar\right) P^{-1}X_1\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/pates/21.png)
pour une matrice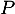 que l'on précisera.
que l'on précisera.
- Calculer la limite de
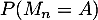 lorsque n tend vers l'infini.
lorsque n tend vers l'infini.
Correction
Correction
Oral ENS ULM - 2019- On peut représenter la situation par un arbre, et on obtient les valeurs suivantes:
![\[P( M_{n+1}=A | M_n=A ) = 1\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/pates_c/1.png)
![\[P( M_{n+1}=B | M_n=A ) = 0\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/pates_c/2.png)
![\[P( M_{n+1}=C | M_n=A ) = 0 \]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/pates_c/3.png)
![\[P( M_{n+1}=A | M_n=B ) = 0 \]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/pates_c/4.png)
![\[P( M_{n+1}=B | M_n=B ) = \dfrac23\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/pates_c/5.png)
![\[P( M_{n+1}=C | M_n=B ) = \dfrac13\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/pates_c/6.png)
![\[P( M_{n+1}=A | M_n=C ) = \dfrac23\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/pates_c/7.png)
![\[P( M_{n+1}=B | M_n=C ) = 0\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/pates_c/8.png)
![\[P( M_{n+1}=C | M_n=C ) = \dfrac13\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/pates_c/9.png)
- La formule des probabilités totales, appliquée au système complet d'événement
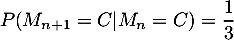 donne
donne
![\[p_{n+1}^A =
P( M_{n+1}=A | M_n=A ) p_n^A
+ P( M_{n+1}=A | M_n=B ) p_n^B
+P( M_{n+1}=A | M_n=C ) p_n^C\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/pates_c/11.png)
soit
![\[p_{n+1}^A = p_n^A + \dfrac23 p_n^C \ \ \ (1)\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/pates_c/12.png)
et de même
![\[p_{n+1}^B =
P( M_{n+1}=B | M_n=A ) p_n^A
+P( M_{n+1}=B | M_n=B ) p_n^B
+P( M_{n+1}=B | M_n=C ) p_n^C\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/pates_c/13.png)
soit
![\[p_{n+1}^B = \dfrac23 p_n^B \ \ \ (2)\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/pates_c/14.png)
et enfin
![\[p_{n+1}^C =
P( M_{n+1}=C | M_n=A ) p_n^A
+P( M_{n+1}=C | M_n=B ) p_n^B
+P( M_{n+1}=C | M_n=C ) p_n^C\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/pates_c/15.png)
soit
![\[p_{n+1}^C = \dfrac{1}{3} p_n^B + \dfrac{1}{3} p_n^C \ \ \ (3)\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/pates_c/16.png)
- On a obtenu en particulier que
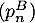 est une suite géométrique de raison
est une suite géométrique de raison  et de premier terme
et de premier terme 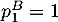 car la première semaine, la personne choisit les pâtes bolognaises.
car la première semaine, la personne choisit les pâtes bolognaises.
On a ainsi
![\[\forall n \in \N^*, p_n^B=\lp\dfrac23\rp^{n-1}\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/pates_c/20.png)
- Les relations (1), (2) et (3) de la question (2) s 'écrivent matriciellement
![\[X_ {n+1}=\lp\begin{array}{ccc}
1& 0 & \dfrac{2}{3} \\[.8em]
0 &\dfrac{2}{3} & 0\\[.8em]
0 & \dfrac{1}{3} & \dfrac{1}{3}
\enar\right) X_n\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/pates_c/21.png)
soit
![\[X_ {n+1}=\dfrac{1}{3}QX_n\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/pates_c/22.png)
- Soit
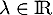 . Pour obtenir les valeurs propres de
. Pour obtenir les valeurs propres de 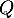 , on cherche les valeurs de
, on cherche les valeurs de 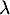 pour lesquelles la matrice
pour lesquelles la matrice 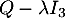 n'est pas inversible.
n'est pas inversible.
![\[Q-\lambda I_3 =\begin{pmatrix}
3-\lambda & 0& 2 \\
0 & 2-\lambda & 0\\
0 & 1 & 1-\lambda\\
\end{pmatrix}\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/pates_c/27.png)
puis, avec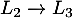 et
et 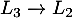
![\[Q-\lambda I_3 \sim \begin{pmatrix}
3-\lambda & 0& 2 \\
0 & 1 & 1-\lambda\\
0 & 2-\lambda & 0 \\
\end{pmatrix}\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/pates_c/30.png)
et enfin, avec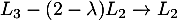
![\[Q-\lambda I_3 \sim \begin{pmatrix}
3-\lambda & 0& 2 \\
0 & 1 & 1-\lambda\\
0 & 0 & (2-\lambda)(\lambda-1) \\
\end{pmatrix}\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/pates_c/32.png)
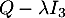 n'est pas inversible lorsque son rang est strictement inférieur à 3, donc pour
n'est pas inversible lorsque son rang est strictement inférieur à 3, donc pour 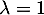 ,
, 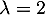 et
et 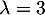 , qui sont donc les 3 valeurs propres de
, qui sont donc les 3 valeurs propres de 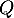 .
.
- Soit
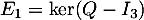 ,
, 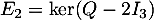 et
et 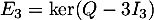 , les espaces propres associés respectivement aux valeurs propres 1, 2 et 3.
On obtient par résolution de système
, les espaces propres associés respectivement aux valeurs propres 1, 2 et 3.
On obtient par résolution de système 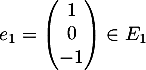 ,
, 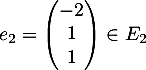 et
et 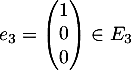 .
.
Dans la base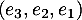 , la matrice
, la matrice 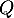 s'écrit :
s'écrit :
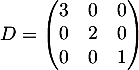
et la formule de changement de base donne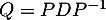
où P est la matrice des vecteurs propres. On obtient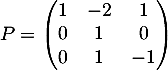
On montre facilement par récurrence que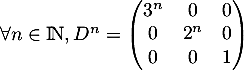 et que
et que 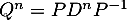 .
.
La relation de la question 3
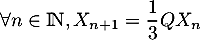
entraîne (par une récurrence immédiate)
![\[\forall n \in \N^*, X_ n=\lp\dfrac13\rp^{n-1}Q^{n-1}X_1\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/pates_c/52.png)
ce qui donne :
![\[\begin{array}{ll}\forall n \in \N^*, X_ n&=P\lp\dfrac13\rp^{n-1}D^{n-1}P^{-1}X_1\\[1.6em]
&=P\begin{pmatrix}
1 & 0& 0 \\
0 & \lp\dfrac23\rp^{n-1} & 0\\
0 & 0 & \lp\dfrac13\rp^{n-1} \\
\end{pmatrix}P^{-1}X_1 \enar\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/pates_c/53.png)
- Avec
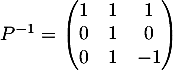
On obtient pour tout entier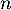 non nul,
non nul,
![\[p_{n}^A = 1-2\times \dfrac{2^{n-1}}{3^{n-1}}+\dfrac{1}{3^{n-1}}\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/pates_c/56.png)
et donc
![\[\lim_{n \to +\infty} P(M_n=A) = \lim_{n \to +\infty} p_n(A) =1\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/pates_c/57.png)
en d'autres termes, au bout d'un certain temps, la personne risque de ne plus manger que des pâtes à l'arrabiata.
Tag:Probabilités conditionnelles - indépendance
Autres sujets au hasard:

Voir aussi: