Formule des probabilités totales
Colle de mathématiques
Sujet de colle de maths:- Probabilités conditionnelles - indépendanceProbabilités conditionnelles - indépendance
Énoncé du sujet
Énoncer et démontrer la formule des probabilités totales.
Correction
(2,3)
\begin{psclip}{\psellipse(0,0)(2,3)}
\psellipse[fillstyle=solid,fillcolor=gray1](0,3)(3,2.3)
\psellipse[fillstyle=solid,fillcolor=gray3](0,-3)(3,2.3)
\end{psclip}
\psellipse(0,0)(2,3)
\psellipse[fillstyle=vlines](0.5,0.2)(1,1.8)
\rput(-1.3,2.7){\large$\Omega$}
\rput(-1.45,1.4){$A_1$}
\rput(-1.65,0){$A_2$}
\rput(-1.45,-1.4){$A_3$}
\psline{<-}(1.3,1.3)(2.,2.6)\rput(2.2,2.7){$B$}
\end{pspicture}\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/excours2_c/1.png)
et
![\[P(B)=P\left( B\cap A_1\rp+P\left( B\cap A_2\rp+P\left( B\cap A_3\rp\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/excours2_c/2.png)
Plus généralement, pour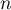
événements 
, 
, …, 
qui forment une partition de l'univers (ou un système complet),
c'est-à-dire deux à deux disjoints et dont la réunion est l'univers, on a,
pour tout événement 
,
![\[\begin{array}{ll}P(B)=P\left( B\cap A_1\rp+P\left( B\cap A_2\rp+\dots+P\left( B\cap A_n\rp \\
=\dsp\sum_{i=1}^n P\left( B\cap A_i\rp\enar\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/excours2_c/8.png)
et donc, en utilisant la définition de la probabilité conditionnelle:
![\[P(B)=\sum_{i=1}^n P\left( A_i\rp\times P_{A_i}\left( B\rp\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/excours2_c/9.png)
La démonstration est immédiate car
![\[B=\left( B\cap A_1\right) \cup \left( B\cap A_2\right) \cup \dots \cup \left( B\cap A_n\right)\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/excours2_c/10.png)
et que les événements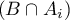
sont deux à deux disjoints.
Correction
Pour trois événements, on peut représenter la situation de la façon suivante:et
Plus généralement, pour
événements , , …, qui forment une partition de l'univers (ou un système complet),
c'est-à-dire deux à deux disjoints et dont la réunion est l'univers, on a,
pour tout événement ,
et donc, en utilisant la définition de la probabilité conditionnelle:
La démonstration est immédiate car
et que les événements
sont deux à deux disjoints.
Tag:Probabilités conditionnelles - indépendance
Autres sujets au hasard:
Voir aussi: