Probabilité de bonne réponse à un QCM
Colle de mathématiques
Sujet de colle de maths:- Probabilités conditionnelles - indépendanceProbabilités conditionnelles - indépendance
Énoncé du sujet
- Soit
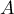 et
et 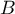 deux événements de probabilités non nulles.
Montrer que
deux événements de probabilités non nulles.
Montrer que
![\[P_B(A)=P_A(B)\dfrac{P(A)}{P(B)}\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/extot1/3.png)
- Un questionnaire à choix multiples propose
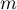 réponses pour chaque question.
réponses pour chaque question.
Soit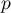 la probabilité qu'un étudiant connaisse la bonne réponse à une question donnée.
S'il ignore la réponse, il choisit au hasard l'une des réponses proposées.
la probabilité qu'un étudiant connaisse la bonne réponse à une question donnée.
S'il ignore la réponse, il choisit au hasard l'une des réponses proposées.
Quelle est pour le correcteur la probabilité qu'un étudiant connaisse vraiment la bonne réponse lorsqu'il l'a donnée ?
Correction
Correction
- Par définition de la probabilité conditionnelle:
![\[P_A(B)=\dfrac{P\left( A\cap B\right)}{P(A)}\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/extot1_c/1.png)
et donc
![\[P_B(A)=\dfrac{P\left( A\cap B\right)}{P(B)}
=\dfrac{P_A(B)\,P(A)}{P(B)}\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/extot1_c/2.png)
-
On note les événements
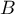 :"L'étudiant donne la bonne réponse" et
:"L'étudiant donne la bonne réponse" et
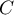 :"L'étudiant connait la bonne réponse".
:"L'étudiant connait la bonne réponse".
On cherche alors .
.
D'après l'énoncé on a: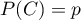 ,
, 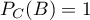 , et
, et 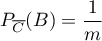 .
.
D'après la formule des probabilités totales, on a alors:
![\[\begin{array}{ll} P(B)&=P\left( B\cap C\right) + P\left( B\cap\overline{C}\right) \\[.7em]
&=P(C)P_C(B)+P\lp\overline{C}\right) P_{\overline{C}}(B)\\[.7em]
&=p+(1-p)\tm\dfrac1m\\[.5em]
&=\dfrac{mp+(1-p)}m\enar\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/extot1_c/9.png)
et enfin, d'après la formule de Bayes, démontrée au a)
![\[\begin{array}{ll}P_B(C)&=P_C(B)\dfrac{P(C)}{P(B)}\\[1em]
&=\dfrac{mp}{mp+(1-p)}\\[.8em]
&=\dfrac{1}{1+\frac{1-p}{mp}}\enar\]](/Generateur-Devoirs/Colles/Probabilites-conditionnelles-independance/extot1_c/10.png)
Tag:Probabilités conditionnelles - indépendance
Autres sujets au hasard:

Voir aussi: