Caractérisation d'une similitude
Colle de mathématiques
Sujet de colle de maths:- Espaces euclidiensEspaces euclidiens, produit scalaire
Énoncé du sujet
Soit  muni du produit scalaire canonique,
muni du produit scalaire canonique,
 et
et  .
On dit que
.
On dit que  est une similitude de rapport
est une similitude de rapport  si pour tout
si pour tout  ,
,  .
.
- Soit
 tels que
tels que  . Démontrer que
. Démontrer que  .
.
- Démontrer que
 est une similitude de rapport
est une similitude de rapport  si et seulement si, pour tous
si et seulement si, pour tous  ,
,

- On souhaite prouver que
 est une similitude si et seulement
est une similitude si et seulement  est non-nulle et conserve l'orthogonalité:
pour tout couple
est non-nulle et conserve l'orthogonalité:
pour tout couple  , si
, si  , alors
, alors  .
.
- Prouver le sens direct.
- Soit
 une base orthonormale de
une base orthonormale de  .
Démontrer que, pour tout couple
.
Démontrer que, pour tout couple  ,
,
 .
.
- Démontrer le sens réciproque.
Correction
Correction
- On a, en utilisant la bilinéarité et la symétrie du produit scalaire,
![\[\begin{array}{ll}\langle u+v,u-v\rangle&=\|u\|^2-
\langle u,v\rangle
+\langle v,u\rangle
-\|v\|^2\\
&=\|u\|^2-\|v\|^2\enar\]](/Generateur-Devoirs/Colles/EspaceEuclidien/similitude_c/1.png)
et ainsi,
![\[\langle u+v,u-v\rangle=0
\iff \|u\|^2=\|v\|^2\]](/Generateur-Devoirs/Colles/EspaceEuclidien/similitude_c/2.png)
- Bien sûr, le sens réciproque est trivial puisqu'il suffit
de choisir
 .
.
Réciproquement, supposons que pour tout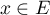 , on a
, on a
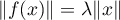 . Alors,
d'une part
. Alors,
d'une part
![\[\begin{array}{ll}
\|f(x+y)\|^2&=\|\lambda(x+y)\|^2\\[.4em]
&=\lambda^2\|x+y\|^2\\[.4em]
&=\lambda^2\langle x+y,x+y\rangle\\[.4em]
&=\lambda^2\Bigl( \|x\|^2+2\langle x,y\rangle +\|y\|^2\Bigr)
\enar\]](/Generateur-Devoirs/Colles/EspaceEuclidien/similitude_c/6.png)
et d'autre part
![\[\begin{array}{ll}\|f(x+y)\|^2&=\langle f(x+y),f(x+y)\rangle\\[.4em]
&=\|f(x)\|^2+2\langle f(x),f(y)\rangle+\|f(y)\|^2\\[.5em]
&=\lambda^2\|x\|^2+2\langle f(x),f(y)\rangle+\lambda^2\|y\|^2\end{array}
\]](/Generateur-Devoirs/Colles/EspaceEuclidien/similitude_c/7.png)
En égalant ces deux dernières relations, on obtient donc
![\[\langle f(x),f(y)\rangle=\lambda^2 \langle x,y\rangle\]](/Generateur-Devoirs/Colles/EspaceEuclidien/similitude_c/8.png)
-
- C'est une conséquence directe de la question précédente.
- On sait que
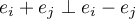 .
Puisque
.
Puisque 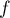 préserve l'orthogonalité,
préserve l'orthogonalité, 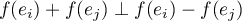 .
Et d'après la première question,
.
Et d'après la première question, 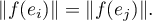
- Soit
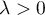 tel que
tel que 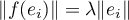 (
(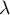 ne dépend pas de
ne dépend pas de  d'après la question précédente, et est strictement
positif sinon
d'après la question précédente, et est strictement
positif sinon 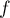 serait nulle).
On va démontrer que
serait nulle).
On va démontrer que 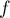 est une similitude de rapport
est une similitude de rapport 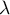 .
Soit
.
Soit 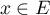 qui s'écrit
qui s'écrit
![\[x=\sum_{i=1}^n x_i e_i\]](/Generateur-Devoirs/Colles/EspaceEuclidien/similitude_c/21.png)
Alors
![\[f(x)=\sum_{i=1}^n x_if(e_i)\]](/Generateur-Devoirs/Colles/EspaceEuclidien/similitude_c/22.png)
La famille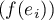 étant orthogonale, on a
étant orthogonale, on a
![\[\begin{array}{lcl}
\|f(x)\|^2&=&\dsp\sum_{i=1}^n |x_i|^2\|f(e_i)\|^2\\
&=&\lambda^2\dsp\sum_{i=1}^n |x_i|^2\\[1.2em]
&=&\lambda^2\|x\|^2.
\enar\]](/Generateur-Devoirs/Colles/EspaceEuclidien/similitude_c/24.png)
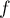 est bien une similitude de rapport
est bien une similitude de rapport 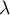 .
.
Tag:Espaces euclidiens
Autres sujets au hasard:

Voir aussi: