Endomorphisme antisymétrique
Colle de mathématiques
Sujet de colle de maths:- Espaces euclidiensEspaces euclidiens, produit scalaire
Énoncé du sujet
Soit  un espace euclidien de dimension
un espace euclidien de dimension  .
Un endomorphisme
.
Un endomorphisme 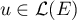 est dit antisymétrique si
est dit antisymétrique si
![\[\forall x,y\in E,\ \langle u(x),y\rangle=-\langle x,u(y)\rangle\]](/Generateur-Devoirs/Colles/EspaceEuclidien/antisym/4.png)
- Montrer que
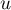 est antisymétrique si et seulement si,
pour tout
est antisymétrique si et seulement si,
pour tout 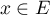 ,
, 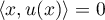 .
.
Dans la suite, est un endomorphisme antisymétrique,
est un endomorphisme antisymétrique,
- Démontrer que
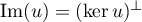 .
.
- Soit
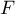 un sous-espace de
un sous-espace de 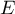 stable par
stable par 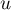 .
Démontrer que
.
Démontrer que  est stable par
est stable par 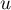 .
.
- Montrer que
 .
.
- Démontrer que le spectre de
 est soit vide, soit restreint à
est soit vide, soit restreint à 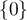 .
.
- Montrer que les valeurs propres de
 sont négatives.
sont négatives.
Correction
Correction
- Si
 est antisymétrique, pour tout
est antisymétrique, pour tout  ,
alors
,
alors 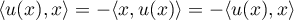 et donc
et donc  .
.
Réciproquement, supposons que pour tout
pour tout 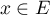 .
.
Soit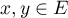 , alors on a
, alors on a
![\[\langle u(x+y),x+y\rangle=0\]](/Generateur-Devoirs/Colles/EspaceEuclidien/antisym_c/8.png)
et alors
![\[\begin{array}{lcl}
0=\langle u(x+y),x+y\rangle
&=&\langle u(x),x\rangle+\langle u(x),y\rangle+\langle u(y),x\rangle+\langle u(y),y\rangle\\[.6em]
&=& \langle u(x),y\rangle+\langle u(y),x\rangle
\enar\]](/Generateur-Devoirs/Colles/EspaceEuclidien/antisym_c/9.png)
ce qui prouve bien que
![\[\langle u(x),y\rangle=-\langle u(y),x\rangle\]](/Generateur-Devoirs/Colles/EspaceEuclidien/antisym_c/10.png)
c'est-à-dire que est antisymétrique.
est antisymétrique.
- Soit
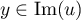 , c'est-à-dire
, c'est-à-dire 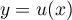 et soit
et soit 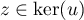 .
.
On a alors
![\[\langle y,z\rangle
=\langle u(x),z\rangle
=-\langle x,u(z)\rangle=0\]](/Generateur-Devoirs/Colles/EspaceEuclidien/antisym_c/15.png)
ce qui montre qu'on on a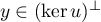 , et donc
que
, et donc
que 
Par ailleurs, on peut aussi raisonner avec les dimensions, et avec le théorème du rang:
![\[\begin{array}{ll}
\dim(\ker u)^\perp&=n-\dim(\ker u)\\
&=n-\bigl(n-\dim(\text{Im}(u))\bigr)\\
&=\dim(\text{Im}(u)
\enar\]](/Generateur-Devoirs/Colles/EspaceEuclidien/antisym_c/18.png)
ce qui finit donc de montrer l'égalité recherchée.
- Soit
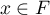 et
et 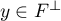 . Alors on a
. Alors on a
![\[\langle u(y),x\rangle=-\langle y,u(x)\rangle=0\]](/Generateur-Devoirs/Colles/EspaceEuclidien/antisym_c/21.png)
puisque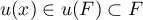 et
et  .
.
- On a toujours
 car
si
car
si 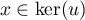 alors
alors  donc
donc 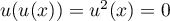 .
.
Réciproquement, soit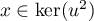 . Alors
. Alors
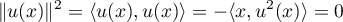
et donc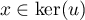 .
.
- Si le spectre de
 n'est pas vide, soit
n'est pas vide, soit 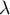 une valeur propre de
une valeur propre de 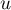 et
et  un vecteur propre (non-nul) associé. Alors
un vecteur propre (non-nul) associé. Alors
![\[\langle u(x),x\rangle=0\]](/Generateur-Devoirs/Colles/EspaceEuclidien/antisym_c/35.png)
alors que l'on a aussi
![\[\langle u(x),x\rangle
=\langle \lambda x,x\rangle=\lambda \|x\|^2\]](/Generateur-Devoirs/Colles/EspaceEuclidien/antisym_c/36.png)
et donc nécessairement .
.
- Soit
 une valeur propre de
une valeur propre de 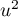 ,
de vecteur propre associé
,
de vecteur propre associé 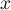 .
.
On a alors
![\[\langle u^2(x),x\rangle=\lambda \|x\|^2\]](/Generateur-Devoirs/Colles/EspaceEuclidien/antisym_c/41.png)
et d'autre part,
![\[\langle u^2(x),x\rangle=-\langle u(x),u(x)\rangle=-\|u(x)\|^2\]](/Generateur-Devoirs/Colles/EspaceEuclidien/antisym_c/42.png)
ce qui prouve bien que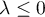 .
.
Tag:Espaces euclidiens
Autres sujets au hasard:

Voir aussi: