Caractériation complexe de l'égalité triangulaire
Colle de mathématiques
Sujet de colle de maths:- ComplexesNombres complexs
Énoncé du sujet
Soit  . Montrer que
. Montrer que
 si et seulement si
si et seulement si
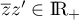 .
.
Correction
 est une égalité
si et seulement si
est une égalité
si et seulement si
 ,
, 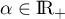 .
Dans ce cas on a alors
.
Dans ce cas on a alors  .
.
Cette condition est aussi suffisante: soit et
et 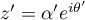 ,
avec
,
avec 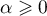 et
et
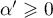 .
.
On a alors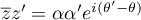 ,
et donc
,
et donc
![$\overline{z}z'\in\R_+\iff \theta\equiv\theta'\,[2\pi]$](/Generateur-Devoirs/Colles/Complexes/ex0.01_c/10.png) d'où
d'où
 et
et
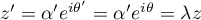 avec
avec 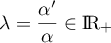 .
.
Correction
L'inégalité triangulaireCette condition est aussi suffisante: soit
On a alors
Tag:Complexes
Autres sujets au hasard:

Voir aussi: