Équation polynomiale de degré 4
Colle de mathématiques
Sujet de colle de maths:Énoncé du sujet
Résoudre dans  , puis dans
, puis dans  , l'équation:
, l'équation:
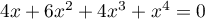 .
.
Correction
![\[(1+x)^4=1+4x+6x^2+4x^3+x^4\]](/Generateur-Devoirs/Colles/Complexes/exEqdeg4.2_c/1.png)
Ici, on a donc
![\[\begin{array}{ll}4x+6x^2+4x^3+x^4=0
&\iff (1+x)^4-1=0 \\[.6em]
&\iff (1+x)^4=1
\enar\]](/Generateur-Devoirs/Colles/Complexes/exEqdeg4.2_c/2.png)
Dans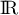 , on a donc
, on a donc
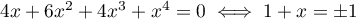 et donc l'équation a deux solutions
et donc l'équation a deux solutions  ou
ou  .
.
Dans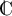 , la formule du binôme reste bien sûr exactes, par contre
, la formule du binôme reste bien sûr exactes, par contre
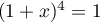 signifie que
signifie que 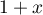 est une racine quatrième de l'unité,
soit
est une racine quatrième de l'unité,
soit
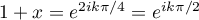 , pour
, pour  ,
, 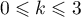 ,
et donc l'équation admet 4 solutions
,
et donc l'équation admet 4 solutions
![\[\mathcal{S}=\la0;\, -1+i,\, -2,\, -1-i \ra\]](/Generateur-Devoirs/Colles/Complexes/exEqdeg4.2_c/13.png)
Correction
On reconnaît presque les coefficients du binôme de Newton:Ici, on a donc
![\[\begin{array}{ll}4x+6x^2+4x^3+x^4=0
&\iff (1+x)^4-1=0 \\[.6em]
&\iff (1+x)^4=1
\enar\]](/Generateur-Devoirs/Colles/Complexes/exEqdeg4.2_c/2.png)
Dans
Dans
Tags:ComplexesSommes
Autres sujets au hasard:

Voir aussi: