Factorisation d'un polynôme bicarré en facteurs réels
Colle de mathématiques
Sujet de colle de maths:Énoncé du sujet
On considère le polynôme
 .
.
- Déterminer les racines de
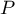 .
.
- En déduire que
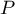 peut s'écire comme le produit
de deux trinômes du second degré à coefficients réels.
peut s'écire comme le produit
de deux trinômes du second degré à coefficients réels.
Correction
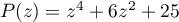 .
.
Correction
On considère le polynôme- On pose
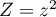 , et
, et 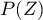 est un trinôme du second degré
de discriminant
est un trinôme du second degré
de discriminant
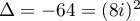 ,
et admet donc deux racines complexes conjuguées
,
et admet donc deux racines complexes conjuguées
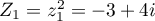 et
et 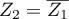 .
.
Soit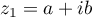 ,
alors
,
alors 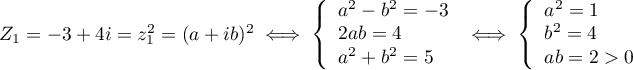 .
.
On trouve donc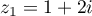 ou
ou 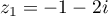 .
.
De même avec , on touve
, on touve
 ou
ou 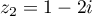 .
.
- On en déduit que
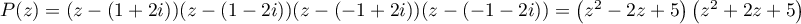
Tags:ComplexesPolynôme
Autres sujets au hasard:

Voir aussi: