Application linéaire sur des polynômes de degré 2 ? Noyau et image ?
Colle de mathématiques
Sujet de colle de maths:- Applications linéairesApplications linéaires
- PolynômePolynômes
Énoncé du sujet
- L'application
![$f:\R_2[X]\to \R^2,\ P\mapsto \big(P(1),P'(1)\big)$](/Generateur-Devoirs/Colles/Applin/exAL5.2/1.png) est-elle linéaire ?
Préciser son noyau et son image. Est-elle injective ? surjective ? bijective ?
est-elle linéaire ?
Préciser son noyau et son image. Est-elle injective ? surjective ? bijective ?
- L'application
![$g:\R_2[X]\to \R^3,\ P\mapsto \big(P(1),P'(1),P''(1)\big)$](/Generateur-Devoirs/Colles/Applin/exAL5.2/2.png) est-elle linéaire ?
Préciser son noyau et son image. Est-elle injective ? surjective ? bijective ?
est-elle linéaire ?
Préciser son noyau et son image. Est-elle injective ? surjective ? bijective ?
Correction
Correction
- Soit
![$P,Q\in\R_2[X]$](/Generateur-Devoirs/Colles/Applin/exAL5.2_c/1.png) et
et 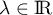 ,
alors d'après les propriétés de linéarité de la dérivation (justement !)
,
alors d'après les propriétés de linéarité de la dérivation (justement !)
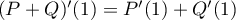 et
et 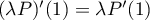 on déduit directement que
on déduit directement que
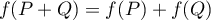 et que
et que
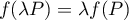 ,
c'est-à-dire que
,
c'est-à-dire que 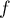 est une application linéaire.
est une application linéaire.
Soit![$P\in\R_2[X]$](/Generateur-Devoirs/Colles/Applin/exAL5.2_c/8.png) tel que
tel que 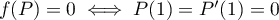 .
Ainsi 1 est une racine double de
.
Ainsi 1 est une racine double de 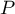 qui peut donc se factorise par
qui peut donc se factorise par  .
.
Comme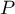 est de degré 2, on en déduit que
est de degré 2, on en déduit que
![\[\text{Ker}(f)=\Bigl\{ a(X-1)^2\,;\,a\in\R\Bigr\}\]](/Generateur-Devoirs/Colles/Applin/exAL5.2_c/13.png)
En particulier,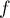 n'est pas injective, et donc pas bijective.
n'est pas injective, et donc pas bijective.
Pour étudier l'image, soit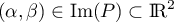 , on cherche
, on cherche ![$P\in\R_2[X]$](/Generateur-Devoirs/Colles/Applin/exAL5.2_c/16.png) tel que
tel que 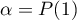 et
et 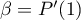 .
.
Il suffit de prendre par exemple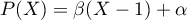 .
.
Ainsi,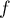 est surjective.
est surjective.
- Comme à la question précédente, l'application est linéaire.
Son noyau est cette fois réduit au polynôme nul, car un polynôme de degré 2 non nul ne peut avoir une racine triple. On en déduit d'une part que l'application est injective, et, d'autre part grâce au théorème du rang, que
![\[\text{rg}(f)=\text{dim}\lp\text{Im}(f)\rp=3\]](/Generateur-Devoirs/Colles/Applin/exAL5.2_c/21.png)
et donc que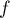 est aussi surjective.
est aussi surjective.
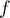 est donc aussi bijective.
est donc aussi bijective.
Tags:Applications linéairesPolynôme
Autres sujets au hasard:

Voir aussi: