Suites numériques

Première générale, spécialité maths


Somme des termes d'une suite

Somme des termes d'une suite arithmétique


Propriété:
La somme des n premiers entiers naturels est:
1+2+3+…+n = n(n+1)/2

Démonstration: On écrit la somme deux façons, en ordonnant les termes de fa¸on croissante et décroissante:
Sn = 1 + 2 + … + (n−1) + n Sn = n + (n−1) + … + 2 + 1
En sommant alors directement, terme à terme, tous les termes valent exactement (n−1) et on on obtient donc
2Sn = (n−1) + (n−1) + … + (n−1)
Cette dernière somme comporte toujours n termes, tous égaux à (n−1), soit donc
2Sn = n×(n−1)
d'où la formule de la propriété en divisant finalement par 2.

Méthode pour calculer une somme de termes d'une suite arithmétique

Par exemple on veut calculer la somme
S = 5+8+11+ … + 35
On détaille chaque terme de la suite arithmétique, ici de raison 3:
S = (5+3×0) + (5+3×1) + … (5+3×10)
Il y donc 11 termes dans cette somme (de 0 à 10), donc 11 fois 5 et on peut factoiser les autres termes par 3:
S = 11×5 + 3×(0+1+2+…+10)
Dans le terme factorisé on reconnaît la somme des premiers entiers de la propriété précédente avec n = 10 , et donc
S = 11×5 + 3×10(10+1)/2 = 220


Exercice 18
Calculer les sommes
  1. S1 = 8+9+10+11+…+50

  2. S2 = 1+3+5+…+31

  3. S3 = 2+4+6+…+32

  4. S4 = 5+10+15+…+55



Somme des termes d'une suite géométrique


Propriété:
Pour tout réel q≠1,
1 + q + q2 + … + qn = 1−qn+1/1−q

Pour q = 1, la somme vaut 1 + q + q2 + … + qn = n+1

Démonstration: quand on multiplie la somme S par la raison q on obtient "presque" la même somme. Plus précisément, pour la différence s'écrit
S−qS = 1 + q + q2 + … + qn − q(1 + q + q2 + … + qn)
ou encore en développant la deuxième partie:
S−qS = 1 + q + q2 + … + qn − q − q2 − … − qn+1
On parle ici de somme téléscopique: presque tous les termes s'annulent entre eux, et il ne reste seulement que
S−qS = 1 − qn+1
Il reste à factoiser le terme de gauche, soit
(1−q)S = 1 − qn+1
et à diviser par (1−q) si q≠1

Méthode pour calculer une somme de termes d'une suite arithmétique

Premier exemple: on veut calculer la somme
S1 = 1 + 2 + 4 + … + 1024
qu'on écrit sous la forme de somme des termes d'une suite géométrique de raison 2:
S1 = 1 + 2 + 22 + … +210
d'où, en utilisant la formule de la propriété précédente,
S1 = 1−210+1/1−2 = 1−211/−1
soit encore
S1 = 211 − 1 = 2027

Deuxième exemple, avec une somme géométrique qui ne démarre pas à 1:
S2 = 8 + 16 + 32 + … + 2048
qu'on factorise dans un premier temps
S2 = 8( 1 + 2 + 4 + … + 256)
qu'on écrit sous la forme de somme des termes d'une suite géométrique de raison 2:
S2 = 8( 1 + 2 + 22 + … + 28)
d'où, en utilisant la formule de la propriété précédente,
S1 = 81−28+1/1−2 = 81−29/−1 = 4088
soit encore

Exercice 19
Calculer les sommes :
  1. S = 4 + 2 + 1 + 0,5 + 0,25 + 0,125 + 0,0625

  2. P = 9 + 3 + 1 + … + 1/36

  3. Q = 3 − 6 + 12 − 24 + … + 3072




Exercice 20
Clément aime la pizza mais n'ose jamais en finir une sans en laisser un peu: à chaque fois, il mange la moitié de ce qu'il reste. La première fois qu'il se sert, il mange donc la moitié de la pizza.
Quelle portion de pizza a-t-il mangé lorsqu'il s'est resservi 5 fois ? Quelle portion reste-t-il alors ?



Exercice 21
Deux amis partent pour une randonnée de 200 km.
Le premier jour, ils parcourent 20 km. Chaque jour, en raison de la fatigue accumulée, leur distance parcourue diminue de 5% par rapport au jour précédent.
Quelle distance auront-ils parcouru au bout de 2 jours ? 5 jours ?
Á l'aide d'une calculatrice ou d'un ordinateur, déterminer le nombre de jours nécessaires pour terminer cette randonnée.



Exercice 22
Soit la suite (un) définie pour tout entier naturel n par un = 3n + 4n − 3 .
On note (vn) et (wn) les suites définies par vn = 3n et wn = 4n−3.
  1. Montrer que (vn) est une suite géométrique et que (wn) est une suite arithmétique
  2. Calculer Vn = v0 + v1 + … + vn0 et Wn = w0 + w1 + … + wn0
  3. En déduire la somme, en fonction de n, Un = u0 + u1 + … + un0



Exercice 23
Soit (un) la suite définie par les deux premiers termes u0 = 1 et u1 = 2 et, pour tout entier naturel n, par la relation de récurrence
un+2 = 1,5 un+1 − 0,5 un
.
    1. Montrer que la suite (vn) définie par vn = un+1−un est géométrique.
    2. Exprimer alors vn en fonction de n.
    1. Calculer en fonction de n la somme
      Sn = 0,5 + 0,52 + 0,53 + … + 0,5n
    2. Exprimer alors un en fonction de n.



Exercice 24
On construit une spirale à partir de demi-cercles de la façon suivante:
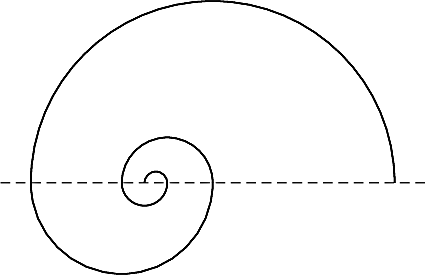
Construction spirale avec des demi-cercles

Le premier demi-cercle a un rayon de 10 cm. Ensuite, chaque demi-cercle a un rayon égal à la moitié du demi-cercle précédent.
  1. Quelle est la longueur de la spirale dessinée sur cette figure ?
  2. Quelle est la longueur de cette spirale avec 10 demi-cercles ? avec 100 ? avec 1000 ? avec 10 000 ?
    Quelle est la limite de la longueur de cette spirale ?
  3. Si on prolonge indéfiniment cette spirale, on constate qu'elle converge vers un point C. Où ce point C se trouve-t-il sur le grand segment initial ?




Voir aussi:
LongPage: h2: 2 - h3: 3