Suites numériques

Première générale, spécialité maths


Suites particulières

Suites arithmétiques

Définition:
Une suite arithmétique est une suite dont chaque terme est obtenu en ajoutant la même quantité r, appelée raison de la suite, au terme précédent.
Pour tout entier n, on a
un+1 = un + r ⇔ un+1 − un = r

Schéma d'une suite arithmétique


Exercice 10
  • Soit la suite (un) définie par u0 = 0 et pour tout entier n par la relation un+1 = un+2.
    Alors, u1 = …, u2 = …, u3 = …, …
    (un) est une suite arithmétique de raison r = ….

  • Soit (un) la suite définie par la relation vn = 5n+1

    Alors, pour tout entier n, on a vn+1−vn = …

    On en déduit que (vn) est une suite arithmétique de raison r = …

  • Soit la suite (wn) définie par la relation wn = n2+2.
    Alors, w1 = …, w2 = …, w3 = …, …
    Cette suite peut-elle être arithmétique ?

  • Soit la suite (xn) définie par x0 = 3 et pour tout entier n par la relation de récurrence xn+1 = 2xn+1.
    Alors, x1 = …, x2 = …, x3 = …, …
    Cette suite peut-elle être arithmétique ?




Propriété
Soit (un) la suite arithmétique de premier terme u0 et de raison r, alors, pour tout entier n, on a
un = u0 + nr
Pour tout entier p quelconque, on a aussi
un = up + (n−p)r


Exercice 11
  • Soit la suite arithmétique (un) de premier terme u0 = −5 et de raison r = 2.
    Calculer u3002.
  • Soit la suite arithmétique (vn) de premier terme u2 = 1200 et de raison r = −10.
    Calculer v25.
    À partir de quel rang la suite est-elle négative ?
  • La suite (un) est arithmétique de raison r = 5 et u25 = 17.
    Calculer u20.
  • La suite (un) est arithmétique et telle que u3 = 18 et u3 + u4 + u5 + u6= 105.
    Quelle est la raison de cette suite ? Quelle est son premier terme u1 ?
  • La suite (un) définie par un = n+5/n+1 est-elle arithmétique ? Si oui, quelle est sa raison ?
  • La suite (un) définie par un = −3n+5/8 est-elle arithmétique ? Si oui, quelle est sa raison ?
  • Soit (un) une suite arithmétique telle que u10 = −70 et u25 = 80.
    Calculer la raison r de cette suite, puis calculer u0 et u1212.



Propriété
Une suite arithmétique de raison r est
  • strictement croissante si r>0
  • strictement décroissante si r<0
  • constante si r = 0.

Démonstration: Comme on a un+1−un = r, le signe de cette différence, donc le sens de variation de la suite, est directement donné par le signe de la raison r.

Exercice 12
Donner le sens de varition des suites arithmétiques (un) suivantes:
  1. un = 4n+2
  2. un = −2n+1/3
  3. u3 = 5 et u17 = 7
  4. u8 = 7/4 et u19 = 3/4
  5. un+1 = un+5



Suites géométriques

Définition:
Une suite géométrique est une suite dont chaque terme est obtenu en multipliant par la même quantité q, appelée raison de la suite, le terme précédent.
Pour tout entier n, on a donc
un+1 = q× un ⇔ un+1/un = q

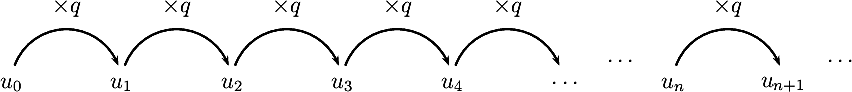
Schéma d'une suite géométrique

Exemples:
  • La suite de nombres 1, 2, 4, 8, 16, 32, … des puissances successives de 2 est la suite géométrique de raison q = 2 et de premier terme u0 = 1.
  • la suite (vn) de terme général vn = (-1)n, pour laquelle v0 = 1, v1 = −1 v2 = 1 v3 = −1, … est la suite géométrique de premier terme v0 = 1 et de raison q = −1.
  • Soit la suite (wn) définie par la relation wn = 2×3n.
    Alors, pour tout entier n, on a
    wn+1/wn = 2×3n+1/2×3n = 3
    et cette suite est donc géométrique de raison q = 3



Propriété
Soit (vn) la suite géométrique de premier terme v0 et de raison q, alors, pour tout entier n, on a
vn = v0 × qn
Pour tout entier p quelconque, on a aussi
vn = vp qn−p


Exercice 13
  • Soit (un) la suite géométrique de premier terme u0 = 0,2 et de raison q = 1/4.
    Calculer u4 et u20.

    On a
    u4 = u0q4 = 0,2×1/44
    et
    u20 = u0q20 = 0,2×1/420
  • Soit (un) une suite géométrique avec u1<0 et u6 = 12 et u8 = 48.
    Calculer u9 et u1.

    On a
    u8 = u6q2
    soit
    48 = 12×q2 ⇔ q2 = 4
    On en déduit que q = 2 ou q = −2.
    Comme de plus le premier terme est négatif, la raison est forcément aussi négative, d'où q = −2.
    On calcule alors les termes suivants:
    u9 = u8 = 48×(−2) = −96
    et
    u6 = u1q5 ⇔ 12 = u1(−2)5
    et on trouve donc
    u1 = 12/−32 = −3/8
  • (un) est géométrique telle que u3 = 8 et u3 + u4 + u5 = 14
    Quelle est la raison de cette suite ?

    Soit r la raison de cette suite, alors on a u4=u3r=8r et u5=u3r2=8r2 d'où on doit avoir
    u3 + u4 + u5 = 14 ⇔ 8 + 8r + 8r2 = 14
    La raison est donc solution de l'équation du second degré
    8r2 + 8r − 6 = 0
    qui a pour discriminant Δ=256=162>0 et admet donc deux solutions r=−3/2 et r=−1/2.


Exercice 14
On utilise une feuille de papier, d'épaisseur e = 0,5mm, que l'on replie successivement en deux.
Quelle est l'épaisseur de la feuille après le premier pliage ? après le deuxième ? après le nème ?
Combien de fois faudrait-il replier cette feuille en deux pour obtenir une épaisseur supérieure à la hauteur de la tour Eiffel (environ 300 m) ?



Exercice 17
Soit (un) la suite définie par u0 = 1/2 et, pour tout entier naturel n, un+1 = un/1+2un
On définit la suite (vn) à partir de (un) par vn = 1/un+1
  1. Calculer v0, v1, v2, et v3 et conjecturer la nature de la suite (vn).
  2. Montrer que la suite (vn) est arithmétique.
    Préciser son premier terme et sa raison.
  3. Exprimer vn en fonction de n, puis un en fonction de n


Exercice 18
Soit (un) la suite définie par u0 = −1 et, pour tout entier naturel n, un+1 = 4un/4−un
On définit la suite (vn) à partir de (un) par la relation vn = 3un+2/un
Montrer que la suite (vn) est arithmétique.
Exprimer alors vn, puis un en fonction de n.



Exercice 19
Soit (un) la suite définie par u0 = −1 et, et, pour tout entier naturel n, un+1 = 1/2un+1/4.
On définit aussi la suite (vn) par vn = un − 1/2
  1. Calculer v0, v1, v2 et v3, et conjecturer la nature de la suite (vn).
  2. Prouver que la suite (vn) est géométrique.
  3. Exprimer vn, puis un, en fonction de n.



Voir aussi:
LongPage: h2: 2 - h3: 2