variations et TVI
Exercice corrigé - Spécialité maths, première générale
On considère la fonction  définie sur
définie sur 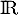 par
par 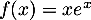
- Étudier le sens de variation de
 .
.
- Montrer que l'équation
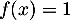 admet une unique solution
sur
admet une unique solution
sur 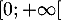 , et en donner une valeur approchée à
, et en donner une valeur approchée à  près.
près.
Correction
On considère la fonction définie sur
définie sur  par
par 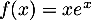
Cacher la correction
On considère la fonction
- On a
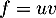 avec
avec  donc
donc 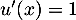 ,
et
,
et 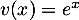 donc
donc 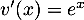 , et alors
, et alors
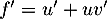 , soit
, soit
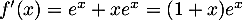 .
.
On a alors
![\[\begin{tabular}{|c|ccccc|}\hline
$x$&$-\infty$&&$-1$&&$+\infty$\\\hline
$e^x$ && $+$ &&$+$&\\\hline
$1+x$ && $-$&0&$+$&\\\hline
$f'(x)$ && $-$&0&$+$&\\\hline
&&&&&\\
$f$ &&\Large{$\searrow$}&&\Large{$\nearrow$}&\\
&&&$-1/e$&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapExponentielle/ex0var_c/11.png)
- Sur
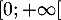 ,
,  est continue (et même dérivable),
strictement croissante, avec
est continue (et même dérivable),
strictement croissante, avec  et
et  .
.
On en déduit, d'après le théorème des valeurs intermédiaires (ou ici le théorème de la bijection) que l'équation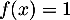 admet une unique solution
admet une unique solution ![$\alpha\in[0;1]$](/Generateur-Devoirs/TS/ChapExponentielle/ex0var_c/17.png) et donc aussi sur
et donc aussi sur 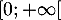 car
car 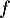 est strictement croissante.
Avec la calculatrice, par balayage, ou dichotomie, on trouve
est strictement croissante.
Avec la calculatrice, par balayage, ou dichotomie, on trouve
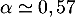
Cacher la correction
Tag:Exponentielle
Voir aussi:
