Sens de variation, produit et composée avec fonction exponentielle (bis)

Exercice corrigé - Spécialité maths, première générale

Énoncé

Étudier le sens de variation de la fonction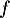

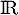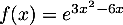définie sur $\R$ par $f(x)=e^{3x^2-6x}$ .

Correction

On a

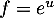ave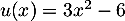c

donc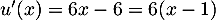

et donc

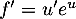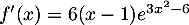
, soit $f'(x)=6(x-1)e^{3x^2-6}$
On peut alors dresser le tableau de variation:

$\begin{tabular}{|c|ccccc|}\hline $x$ & $-\infty$ && 1 && $+\infty$\\\hline $6(x-1)$ && $-$ &\zb&$+$&\\\hline $e^{3x^2-6}$ && $+$ &$|$ & $+$ &\\\hline $f'(x)$ && $-$ &\zb&$+$&\\\hline &&&&&\\ $f$&&\Large{$\searrow$}&&\Large{$\nearrow$}&\\ &&&$e^{-3}$&&\\\hline \end{tabular}$

Tag:Exponentielle

Autres sujets au hasard:

Voir aussi: