Variation d'une fonction rationnelle
Exercice corrigé - Spécialité maths, première générale
Dresser le tableau de variation de la fonction  définie sur
définie sur 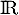 par
par
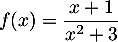 .
.
Correction
On considère la fonction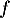 définie sur
définie sur 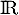 par
par
 .
.
On a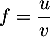 ,
avec
,
avec
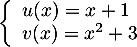 soit
soit
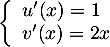 ,
et donc,
,
et donc,
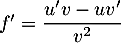 ,
,
![\[\begin{array}{ll}f'(x)
&=\dfrac{1\left( x^2+3\rp-\left( x+1\rp\left( 2x\rp}{(x^2+3)}\\
&=\dfrac{-x^2-2x+3}{(x^2+3)}
\enar\]](/Generateur-Devoirs/1S/Chap3/exvar_c/8.png)
Le trinôme du numérateur a pour discriminant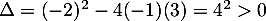 ,
et admet donc deux racines
,
et admet donc deux racines 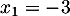 et
et 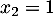 .
.
![\[\begin{tabular}{|c|ccccccc|}\hline
$x$ & $-\infty$ && $-3$ && $1$ &&$+\infty$ \\\hline
$-x^2-2x+3$ && $-$ & \mbox{$0\hspace{-0.67em}\mid$} & $+$ & \mbox{$0\hspace{-0.67em}\mid$} & $-$ &\\\hline
$\left( x^2+3\rp$ && $+$ & $|$ & $+$ & $|$ & $+$ &\\\hline
$f'(x)$ && $-$ & \mbox{$0\hspace{-0.67em}\mid$} & $+$ & \mbox{$0\hspace{-0.67em}\mid$} & $-$ &\\\hline
&&&&&$\frac12$&&\\
$f$ && \psline{->}(-0.6,0.4)(0.3,-0.4)
&&\psline{->}(-0.4,-0.4)(0.4,0.4)
&&
\psline{->}(-0.3,0.4)(0.6,-0.4)&
\\
&&&$-\frac16$&&&&\\\hline
\end{tabular}
\]](/Generateur-Devoirs/1S/Chap3/exvar_c/12.png)
Cacher la correction
On considère la fonction
On a
![\[\begin{array}{ll}f'(x)
&=\dfrac{1\left( x^2+3\rp-\left( x+1\rp\left( 2x\rp}{(x^2+3)}\\
&=\dfrac{-x^2-2x+3}{(x^2+3)}
\enar\]](/Generateur-Devoirs/1S/Chap3/exvar_c/8.png)
Le trinôme du numérateur a pour discriminant
![\[\begin{tabular}{|c|ccccccc|}\hline
$x$ & $-\infty$ && $-3$ && $1$ &&$+\infty$ \\\hline
$-x^2-2x+3$ && $-$ & \mbox{$0\hspace{-0.67em}\mid$} & $+$ & \mbox{$0\hspace{-0.67em}\mid$} & $-$ &\\\hline
$\left( x^2+3\rp$ && $+$ & $|$ & $+$ & $|$ & $+$ &\\\hline
$f'(x)$ && $-$ & \mbox{$0\hspace{-0.67em}\mid$} & $+$ & \mbox{$0\hspace{-0.67em}\mid$} & $-$ &\\\hline
&&&&&$\frac12$&&\\
$f$ && \psline{->}(-0.6,0.4)(0.3,-0.4)
&&\psline{->}(-0.4,-0.4)(0.4,0.4)
&&
\psline{->}(-0.3,0.4)(0.6,-0.4)&
\\
&&&$-\frac16$&&&&\\\hline
\end{tabular}
\]](/Generateur-Devoirs/1S/Chap3/exvar_c/12.png)
Cacher la correction
Tag:Fonctions et dérivées
Voir aussi:
