Suite géométrique
Exercice corrigé - Spécialité maths, première générale
Soit 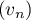 une suite géométrique telle que
une suite géométrique telle que
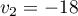 et
et 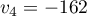 .
.
Déterminer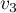 ,
, 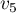 .
.
Déterminer
Correction
Soit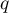 la raison de
la raison de 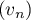 alors on a
alors on a
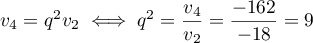 .
.
On en déduit que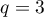 ou
ou 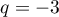 .
.
On a alors soit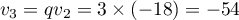 et
et 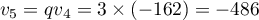
ou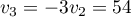 et
et 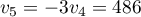 .
.
Cacher la correction
Soit
On en déduit que
On a alors soit
ou
Cacher la correction
Tag:Suites
Voir aussi:
