Suite définie par récurrence et suite intermédiaire géométrique
Exercice corrigé - Spécialité maths, première générale
On considère la suite 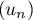 définie par son premier terme
définie par son premier terme
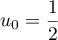 et par la relation, pour tout entier naturel
et par la relation, pour tout entier naturel 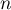 ,
,
 .
.
- Calculer
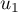 et
et 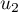 .
.
- Montrer que
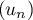 n'est ni arithmétique, ni géométrique.
n'est ni arithmétique, ni géométrique.
- On pose, pour tout entier naturel
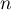 ,
,
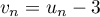 .
.
- Montrer que
 est une suite géométrique,
dont on précisera le premier terme et la raison.
est une suite géométrique,
dont on précisera le premier terme et la raison.
- Exprimer
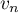 en fonction de
en fonction de  .
.
- En déduire l'expression de
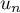 en fonction de
en fonction de 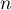 .
.
- Montrer que
Correction
Cacher la correction
-
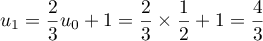 et
et

-
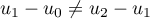 et donc la suite ne peut pas être arithmétique.
et donc la suite ne peut pas être arithmétique.
De même et donc cette suite ne peut pas être géométrique non plus.
et donc cette suite ne peut pas être géométrique non plus.
- On pose, pour tout entier naturel
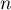 ,
,
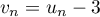 .
.
- Pour tout entier
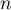 , on a
, on a
![\[\begin{array}{ll}v_{n+1}&=u_{n+1}-3\\[.5em]&=\dfrac23u_n+1-3=\dfrac23u_n-2\\[.8em]&=\dfrac23\left( u_n-3\right)
=\dfrac23v_n\enar\]](/Generateur-Devoirs/1S/Chap9/ex3.2_c/8.png)
ce qui montre que la suite est géométrique de raison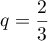 et de premier terme
et de premier terme 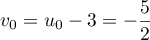 .
.
- On a alors, pour tout entier
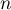 ,
,
![\[v_n=v_0q^n=-\dfrac52\lp\dfrac23\rp^n\]](/Generateur-Devoirs/1S/Chap9/ex3.2_c/12.png)
et alors
![\[u_n=v_n+3=-\dfrac52\lp\dfrac23\rp^n+3\]](/Generateur-Devoirs/1S/Chap9/ex3.2_c/13.png)
- Pour tout entier
Cacher la correction
Tag:Suites
Voir aussi:
