Sens de variation, produit avec fonction exponentielle
Exercice corrigé - Spécialité maths, première générale
Étudier le sens de variation de la fonction 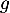 définie par
définie par
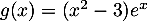
Correction
On a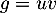 avec
avec 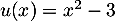 donc
donc 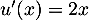 et
et 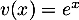 donc
donc 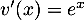 .
.
Ainsi,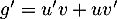 , soit
, soit
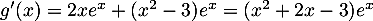
On a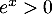 et le premier terme est du second degré de discriminant
et le premier terme est du second degré de discriminant 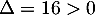 et admet donc deux racines
et admet donc deux racines 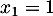 et
et 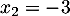 .
.
![\[\begin{tabular}{|c|ccccccc|}\hline
$x$ & $-\infty$ && $-3$ && 1 &&$+\infty$ \\\hline
$x^2+2x-3$ && $+$ &\mbox{$0\hspace{-0.67em}\mid$} & $-$ &\mbox{$0\hspace{-0.67em}\mid$}& $+$ &\\\hline
$e^x$ && $+$&$|$& $+$ & $|$ & $+$&\\\hline
$g'(x)$ && $+$ &\mbox{$0\hspace{-0.67em}\mid$} & $-$ &\mbox{$0\hspace{-0.67em}\mid$}& $+$ &\\\hline
&&&&&&&\\
$g$&&\Large{$\nearrow$}&&\Large{$\searrow$}&&\Large{$\nearrow$}&\\
&&&&&&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/1S/ChapExp/exvarproduit_c/12.png)
Cacher la correction
On a
Ainsi,
On a
![\[\begin{tabular}{|c|ccccccc|}\hline
$x$ & $-\infty$ && $-3$ && 1 &&$+\infty$ \\\hline
$x^2+2x-3$ && $+$ &\mbox{$0\hspace{-0.67em}\mid$} & $-$ &\mbox{$0\hspace{-0.67em}\mid$}& $+$ &\\\hline
$e^x$ && $+$&$|$& $+$ & $|$ & $+$&\\\hline
$g'(x)$ && $+$ &\mbox{$0\hspace{-0.67em}\mid$} & $-$ &\mbox{$0\hspace{-0.67em}\mid$}& $+$ &\\\hline
&&&&&&&\\
$g$&&\Large{$\nearrow$}&&\Large{$\searrow$}&&\Large{$\nearrow$}&\\
&&&&&&&\\\hline
\end{tabular}\]](/Generateur-Devoirs/1S/ChapExp/exvarproduit_c/12.png)
Cacher la correction
Tag:Exponentielle
Voir aussi:
