Sens de variation d'une suite
Exercice corrigé - Spécialité maths, première générale
On considère la suite 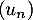 définie par
définie par 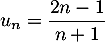 .
.
- Calculer les premiers termes
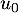 ,
, 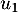 et
et 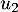 .
.
- Déterminer, pour tout entier
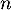 , le signe de
, le signe de 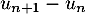 .
.
Donner alors le sens de variation de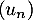 .
.
Correction
On considère la suite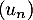 définie par
définie par 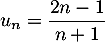 .
.
Cacher la correction
On considère la suite
-
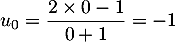 ;
;
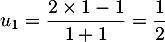 ;
;
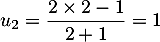
- Pour tout entier
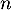 ,
,
![\[\begin{array}{ll}
u_{n+1}-u_n&=\dfrac{2(n+1)-1}{(n+1)+1}-\dfrac{2n-1}{n+1}\\[1em]
&=\dfrac{2n+1)}{n+2}-\dfrac{2n-1}{n+1}\\[1em]
&=\dfrac{(2n+1)(n+1)-(2n-1)(n+2)}{(n+2)(n+1)}\\[1em]
&=\dfrac{3}{(n+2)(n+1)}
\enar\]](/Generateur-Devoirs/1S/Chap9/exvar0_c/7.png)
Comme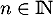 , on a en particulier
, on a en particulier 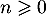 et donc
et donc 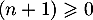 et
et 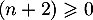 .
.
En particulier, on a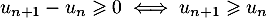 ce qui montre que la suite
ce qui montre que la suite 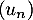 est croissante.
est croissante.
Cacher la correction
Tag:Suites
Voir aussi:
