Sens de variation d'une suite définie par une fonction (bis)
Exercice corrigé - Spécialité maths, première générale
Énoncé
Soit la suite 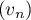 définie pour tout entier naturel
définie pour tout entier naturel 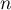 par
par
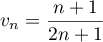 .
.
Déterminer le sens de variation de la suite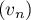 .
.
Déterminer le sens de variation de la suite
Correction
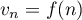 avec la fonction
avec la fonction
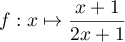 .
.
On a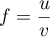 avec
avec
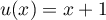 donc
donc 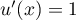 et
et 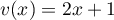 donc
donc 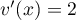 .
.
Ainsi,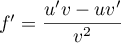 ,
soit
,
soit
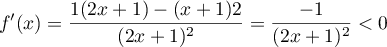 .
.
Ainsi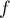 est strictement décroissante sur
est strictement décroissante sur 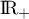 ,
et
,
et 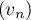 est strictement décroissante sur
est strictement décroissante sur 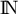 .
.
Correction
On aOn a
Ainsi,
Ainsi
Tag:Suites
Voir aussi:
