Deux fonctions définies à une constante près
Exercice corrigé - Spécialité maths, première générale
Soit 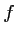 et
et 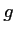 les fonction définies sur
les fonction définies sur
 par:
par:
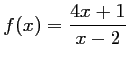 et
et
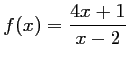 et
et
- Calculer
 et
et  pour tout
pour tout
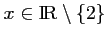 .
.
Que remarque-t-on ?
- Calculer
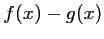 .
Justifier alors la remarque précédente.
.
Justifier alors la remarque précédente.
Correction
Cacher la correction
-
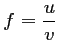 avec
avec
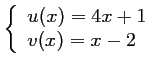 et donc,
et donc,
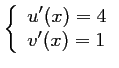
On a alors,
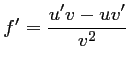 , soit
pour tout
, soit
pour tout
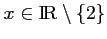 ,
,
 .
.
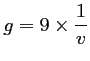 avec
avec 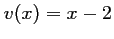 , donc
, donc  , et alors,
pour tout
, et alors,
pour tout
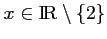 ,
,
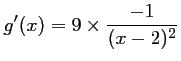 .
.
On remarque que pour tout
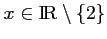 ,
,
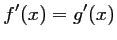 .
.
- Pour tout
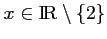 ,
,
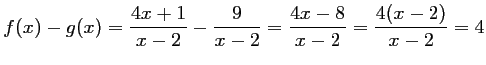 .
.
Ainsi,
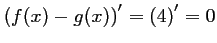 .
.
Or,
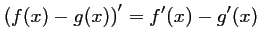 , et on en retrouve alors que
, et on en retrouve alors que
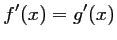 .
.
Cacher la correction
Tag:Fonctions et dérivées
Voir aussi:
