Etats stable et excité de l'atome d'hydrogène
Exercice corrigé - Maths expertes, terminale générale
Énoncé
Un atome d'hydrogène peut se trouver dans deux états différents, l'état stable (S)
et l'état excité (E).
À chaque nanoseconde, la probabilité qu'un atome passe de l'état stable à l'état excité est 0,01.
Mais on ne connaît pas en revanche, la probabilité de changement de l'état excité à l'état stable.
On note par la suite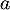 
cette probabilité supposée constante, et 
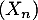la chaîne de Markov décrivant les états de l'atome.
cette probabilité supposée constante, et la chaîne de Markov décrivant les états de l'atome.
- Donner, en fonction de
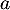, la matrice de transition de la chaîne 
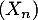associée aux états S et E.
- Après un temps très long, on observe que la proportion d'atomes excités se stabilise autour de 2%.
Déterminer la valeur de
.
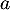Correction
Correction
- La matrice de transition est
.
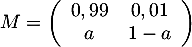- L'état observé sur le long terme est l'état stable
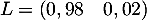qui vérifie
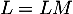, soit
![\[\la\begin{array}{rcrcr}
0,98&=&0,98\tm0,99 &+& 0,02a\\
0,02&=&0,98\tm0,01 &+& 0,02(1-a)
\enar\right.\]](/Generateur-Devoirs/Mex/markov/exH_c/4.png)
Ces deux équations sont équivalentes, et équivalentes à
![\[0,98\tm0,01-0,02a=0\iff a=0,49\]](/Generateur-Devoirs/Mex/markov/exH_c/5.png)
Ainsi, chaque nanoseconde, 49% des atomes dans l'état excités reviennent dans leur état stable.
Tag:Chaines de Markov
Autres sujets au hasard:
Voir aussi:
Quelques devoirs
sur les graphes et chaînes de Markov. Evolution probabiliste et états stables. Traffic aérien entre 4 villes et équilibre de gaz entre deux réservoirs