Des calculs avec des racines 5èmes de l'unité

Exercice corrigé - Maths expertes, terminale générale

Énoncé

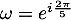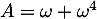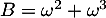On note $\omega=e^{i\frac{2\pi}5}$ et les sommes $A=\omega+\omega^4$ et $B=\omega^2+\omega^3$.
  1. Calculer la somme $1+A+B$.
  2. Exprimer le produit 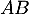$AB$ en fonction de $A$ et $B$.
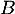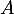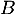  3. En déduire les valeurs de $A$ et $B$. On supposera ici que $A>0$.
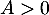  4. Montrer que 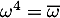$\omega^4=\overline{\omega}$. Déduire alors de ce qui précède la valeur exacte de $\cos\lp\dfrac{2\pi}5\rp$.



Correction

Correction

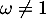  1. On a la somme des termes d'une suite géométrique de raison $\omega\not=1$:
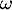    \[\begin{array}{ll}1+A+B&=1+\omega+\omega^2+\omega^3+\omega^4\\ &=\dfrac{1-\omega^5}{1-\omega}\enar\]

    avec $\omega$ qui est une racine 5-ième de l'unité:
    \[\omega^5=\left( e^{i\frac{2\pi}5}\rp^5=e^{5\times i\frac{2\pi}5}=e^{i2\pi}=1\]

    d'où la somme
    \[1+A+B=0\]


  2. On développe le produit
    \[AB=(\omega+\omega^4)(\omega^2+\omega^3)=\omega^3+\omega^4+\omega^6+\omega^7\]

    or, comme $\omega^5=1$, on a
    \[\omega^6=\omega^5\omega=1\omega=\omega\]

    et
    \[\omega^7=\omega^5\omega^2=1\omega^2=\omega^2\]

    et ainsi,
    \[AB=\omega^3+\omega^4+\omega+\omega^2=A+B\]


  3. On a donc trouvé dans les questions précédentes que
    \[\la\begin{array}{ll}1+A+B=0\\AB=A+B\enar\right.\iff\la\begin{array}{ll}A+B=-1\\AB=A+B=-1\enar\right.\]

    La première équation donne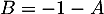 $B=-1-A$, et alors la deuxième équation se réécrit
    \[A(-1-A)=-1\iff A^2+A-1=0\]

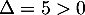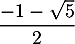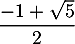    Cette équation du second degré a pour discriminant $\Delta=5>0$ et admet donc deux racines, $\dfrac{-1-\sqrt5}2$ et $\dfrac{-1+\sqrt5}2$.
    Comme on suppose que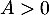 $A>0$, on a donc que $A=\dfrac{-1+\sqrt5}2$, et alors
    \[B=-1-A=-1-\dfrac{-1+\sqrt5}2=\dfrac{-1-\sqrt5}2\]


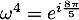  4. On a $\omega^4=e^{i\frac{8\pi}5}$ et
    \[\dfrac{8\pi}5=\dfrac{10\pi}5-\dfrac{2\pi}5=2\pi-\dfrac{2\pi}5\]

    donc
    \[\omega^4=e^{i\lp2\pi-\dfrac{2\pi}5\right)}=e^{i2\pi}e^{-i\frac{2\pi}5} =1e^{-i\frac{2\pi}5}=\overline{\omega}\]

    car $\overline{e^{i\theta}}=e^{-i\theta}$

    On a alors que
    \[\begin{array}{ll}A&=\omega+\omega^4\\&=\omega+\overline{\omega}\\ &=2\cos\lp\dfrac{2\pi}5\rp\enar\]

    et comme on a déjà trouvé que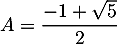 $A=\dfrac{-1+\sqrt5}2$, on obtient maintenant la valeur du cosinus:
    \[\cos\lp\dfrac{2\pi}5\rp=\dfrac{-1+\sqrt5}4\]



    Remarque: comme on trouve que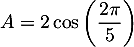 $A=2\cos\lp\dfrac{2\pi}5\rp$ et que 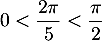$0<\dfrac{2\pi}5<\dfrac\pi2$, on justifie bien l'hypothèse faite sur 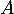$A$, à savoir que $A>0$.


Tag:Polynomes complexes

Autres sujets au hasard: Lancer de dés


Voir aussi:

Quelques devoirs


LongPage: h2: 3 - h3: 0
Énoncé