Factorisation et racines d'un polynôme du 4ème degré

Exercice corrigé - Maths expertes, terminale générale

Énoncé

On considère le polynôme 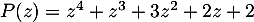$P(z)=z^4+z^3+3z^2+2z+2$.
  1. Montrer que 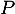$P$ se factorise par 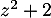$z^2+2$ et factoriser 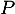$P$ ainsi.
  2. Déterminer dans 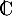$\C$ les racines du polynôme $P$.



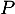Correction

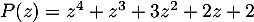
Correction

$P(z)=z^4+z^3+3z^2+2z+2$
  1. On cherche à factoriser le polynôme 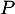$P$ suivant
    \[P(z)=(z^2+2)Q(z)\]

    Le polynôme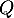 $Q$ est ici de degré au plus 2, et on peut le déterminer par identification ou avec une division euclidienne.

    Division euclidienne:
    \[\begin{array}{ll}z^4+z^3+3z^2+2z+2 &\psline(-.1,.3)(-.1,-3.6) z^2+2\\ z^4\hspace{2.15em}+2z^2 &\psline(0,.4)(2,.4) z^2+z+1 \\[.4em] \psline(0,.5)(2.5,.5) \hspace*{2.2em}z^3+\ z^2+2z+2\\ \hspace*{2.2em}z^3\hspace{2.5em}+2z\\[.4em] \psline(.8,.5)(4.3,.5) \hspace*{4.6em}z^2\hspace{2.4em}+2\\ \hspace*{4.6em}z^2\hspace{2.4em}+2\\ \psline(1,.4)(4.3,.4) \hspace*{9.2em}0\hspace*{1em}\enar\]

    ce qui nous donne donc la factorisation
    \[P(z)=(z^2+2)(z^2+z+1)\]



    Identification: Comme le polynôme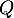 $Q$ recherché est de degré 2, il s'écrit sous la forme 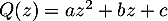$Q(z)=az^2+bz+c$ et il reste à déterminer ses trois coefficients.
    On développe la factorisation recherchée:
    \[\begin{array}{ll}P(z)&=(z^2+2)(az^2+bz+c)\\ &=az^4+bz^3+(2a+c)z^2+2bz+2c \enar\]

    et comme il s'agit toujours du même polynôme
    \[P(z)=z^4+z^3+3z^2+2z+2\]

    on identifie les coefficients
    \[\la\begin{array}{ll}a=1\\ b=1\\ 2a+c=3\\ 2b=2\\ 2c=2\enar\right.\]

    ce qui nous donne les coefficients:
    \[\la\begin{array}{ll} a&=1\\ b&=1\\ c&1 \enar\right.\]

    et on a donc trouvé la factorisation
    \[P(z)=(z^2+2)(z^2+z+1)\]


  2. On cherche alors toutes les racines de 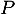$P$, c'est-à-dire les solutions de l'équation 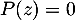$P(z)=0$, soit, pour le produit nul,
    \[z^2+2=0\iff z^2=-2 \iff z=\pm i\sqrt2\]

    soit
    \[z^2+z+1=0\]

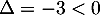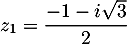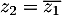    Cette équation du second degré a pour discriminant $\Delta=-3<0$ et admet donc deux racines complexes conjuguées, $z_1=\dfrac{-1-i\sqrt3}2$ et $z_2=\overline{z_1}$.

    En résumé, le polynôme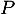 $P$ admet quatre racines
    \[\la-i\sqrt2; i\sqrt2; \dfrac{-1-i\sqrt3}2;\dfrac{-1+i\sqrt3}2\ra\]




Tag:Polynomes complexes

Autres sujets au hasard: Lancer de dés


Voir aussi:

Quelques devoirs


LongPage: h2: 3 - h3: 0