Probabilités: annales de bac et corrections
Terminale générale, spécialité mathématiques
Annales de bac: sujets et corrigés d'exercices posés au baccalauréat en mathématiques sur les probabilités: arbre de probabilités, probabilités conditionnelles, loi binomiale
Exercice 1: Bac 2008, Nouvelle Calédonie - Arbre, arbre à inverser, loi binomiale
Deux éleveurs produisent une race de poissons d'ornement qui ne prennent leur couleur définitive qu'à l'âge de trois mois :
Une animalerie achète les alevins, à l'âge de deux mois : 60 % au premier éleveur, 40 % au second.
Nouvelle Calédonie, mars 2008
On note les événement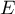 : "le poisson provient du premier élevage",
: "le poisson provient du premier élevage",
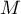 : "le poisson n'a pas survécu",
: "le poisson n'a pas survécu",
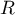 : "le poisson est devenu rouge"
et
: "le poisson est devenu rouge"
et 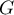 : "le poisson est devenu gris.
: "le poisson est devenu gris.
On peut alors construire l'arbre pondéré suivant:

Cacher la correction
- pour les alevins du premier élevage, entre l'âge de deux mois et l'âge de trois mois, 10 % n'ont pas survécu, 75 % deviennent rouges et les 15 % restant deviennent gris.
- pour les alevins du deuxième élevage, entre l'âge de deux mois et l'âge de trois mois, 5 % n'ont pas survécu, 65 % deviennent rouges et les 30 % restant deviennent gris.
- Un enfant achète un poisson le lendemain de son arrivée à l'animalerie, c'est-à-dire à l'âge de deux mois.
- Montrer que la probabilité que le poisson soit toujours vivant un mois plus tard est de
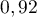 .
.
- Déterminer la probabilité qu'un mois plus tard le poisson soit rouge.
- Sachant que le poisson est gris à l'âge de trois mois, quelle est la probabilité qu'il provienne du premier élevage ?
- Montrer que la probabilité que le poisson soit toujours vivant un mois plus tard est de
- Une personne choisit au hasard et de façon indépendante
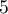 alevins de deux mois. Quelle est la probabilité qu'un mois plus tard, seulement trois soient en vie ? On donnera une valeur approchée à
alevins de deux mois. Quelle est la probabilité qu'un mois plus tard, seulement trois soient en vie ? On donnera une valeur approchée à 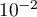 près.
près.
- L'animalerie décide de garder les alevins jusqu'à l'âge de trois mois, afin qu'ils soient vendus avec leur couleur définitive. Elle gagne
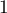 euro si le poisson est rouge,
euro si le poisson est rouge, 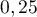 euro s'il est gris et perd
euro s'il est gris et perd 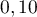 euro s'il ne survit pas.
euro s'il ne survit pas.
Soit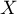 la variable aléatoire égale au gain algébrique de l'animalerie par poisson acheté. Déterminer la loi de probabilité de
la variable aléatoire égale au gain algébrique de l'animalerie par poisson acheté. Déterminer la loi de probabilité de 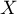 et son espérance mathématique, arrondie au centime.
et son espérance mathématique, arrondie au centime.
Correction exercice 1
Nouvelle Calédonie, mars 2008
On note les événement
On peut alors construire l'arbre pondéré suivant:

-
- La probabilité que l'alevin acheté par l'enfant soit vivant
au bout de trois mois est d'après l'arbre (ou la formule des probabilités totales):
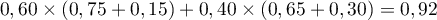
- De même la probabilité pour l'enfant d'avoir un poisson rouge est:
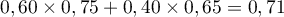
- La probabilité que le poisson provienne du premier élevage sachant qu'il est gris est:
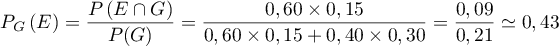
- La probabilité que l'alevin acheté par l'enfant soit vivant
au bout de trois mois est d'après l'arbre (ou la formule des probabilités totales):
- On répète
 fois l'expérience "choisir au hasard un alevin",
dont le succès est "l'alevin est toujours en vie au bout d'un mois"
et de probabilité
fois l'expérience "choisir au hasard un alevin",
dont le succès est "l'alevin est toujours en vie au bout d'un mois"
et de probabilité 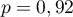 .
Ces expériences sont supposées identiques et indépendantes entre elles.
.
Ces expériences sont supposées identiques et indépendantes entre elles.
Ainsi, la variable aléatoire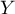 égale au nombre de succès,
c'est-à-dire d'alevins en vie au bout d'un mois sur ces 5 pris au
hasard, suit la loi binomiale de paramètres
égale au nombre de succès,
c'est-à-dire d'alevins en vie au bout d'un mois sur ces 5 pris au
hasard, suit la loi binomiale de paramètres 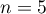 et
et 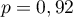 .
.
La probabilité qu'au bout d'un mois trois soient en vie est alors:
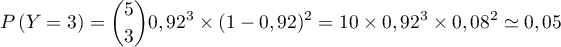
- On a le tableau de loi de probabilité suivant :
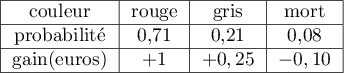
On a donc E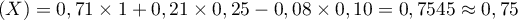 euro.
euro.
Cacher la correction
Exercice 2: Bac 2013, Amérique du Sud - Arbre, loi binomiale, intervalle de fluctuation
Dans cet exercice, les résultats seront arrondis à 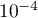 près.
près.
Partie A
En utilisant sa base de données, la sécurité sociale estime que la proportion de Français présentant, à la naissance, une malformation cardiaque de type anévrisme est de 10%. L'étude a également permis de prouver que 30% des Français présentant, à la naissance, une malformation cardiaque de type anévrisme, seront victimes d'un accident cardiaque au cours de leur vie alors que cette proportion n'atteint plus que 8% pour ceux qui ne souffrent pas de cette malformation congénitale.
On choisit au hasard une personne dans la population française et on considère les évènements :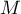 : « La personne présente, à la naissance, une malformation cardiaque de type anévrisme »
: « La personne présente, à la naissance, une malformation cardiaque de type anévrisme »
 : « La personne est victime d'un accident cardiaque au cours de sa vie ».
: « La personne est victime d'un accident cardiaque au cours de sa vie ».
Partie B
La sécurité sociale décide de lancer une enquête de santé publique, sur ce problème de malformation cardiaque de type anévrisme, sur un échantillon de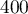 personnes, prises au hasard dans la population française.
On note
personnes, prises au hasard dans la population française.
On note 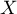 la variable aléatoire comptabilisant le nombre de personnes de l'échantillon présentant une malformation cardiaque de type anévrisme.
la variable aléatoire comptabilisant le nombre de personnes de l'échantillon présentant une malformation cardiaque de type anévrisme.
Partie C
Partie A
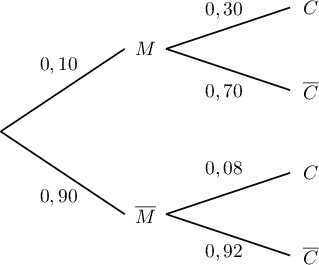
On peut construire l'arbre pondéré suivant:
Partie B
Partie C
Cacher la correction
Partie A
En utilisant sa base de données, la sécurité sociale estime que la proportion de Français présentant, à la naissance, une malformation cardiaque de type anévrisme est de 10%. L'étude a également permis de prouver que 30% des Français présentant, à la naissance, une malformation cardiaque de type anévrisme, seront victimes d'un accident cardiaque au cours de leur vie alors que cette proportion n'atteint plus que 8% pour ceux qui ne souffrent pas de cette malformation congénitale.
On choisit au hasard une personne dans la population française et on considère les évènements :
-
- Montrer que
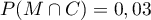 .
.
- Calculer
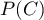 .
.
- Montrer que
- On choisit au hasard une victime d'un accident cardiaque. Quelle est la probabilité qu'elle présente une malformation cardiaque de type anévrisme ?
Partie B
La sécurité sociale décide de lancer une enquête de santé publique, sur ce problème de malformation cardiaque de type anévrisme, sur un échantillon de
- Définir la loi de la variable aléatoire
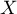 .
.
- Déterminer
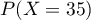 .
.
- Déterminer la probabilité que
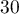 personnes de ce groupe, au moins, présentent une malformation cardiaque de type anévrisme.
personnes de ce groupe, au moins, présentent une malformation cardiaque de type anévrisme.
Partie C
- On considère la variable aléatoire
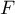 , définie par
, définie par 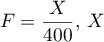 étant la variable aléatoire de
la partie B.
Déterminer l'intervalle de fluctuation asymptotique de la variable aléatoire
étant la variable aléatoire de
la partie B.
Déterminer l'intervalle de fluctuation asymptotique de la variable aléatoire 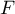 au seuil de
au seuil de 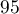 %.
%.
- Dans l'échantillon considéré,
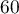 personnes présentent une malformation cardiaque de type anévrisme.
Qu'en pensez-vous ?
personnes présentent une malformation cardiaque de type anévrisme.
Qu'en pensez-vous ?
Correction exercice 2
Partie A
On peut construire l'arbre pondéré suivant:

-
-
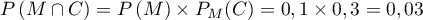
- En utilisant l'arbre (ou d'après la formule des probabilités totales):
![\begin{array}{ll}
P(C)&=P\left( M \cap C\right) + P\left(\overline M \cap C\right)\\[0.3cm]
&= P(M)\times P_M(C) + P\lp\overline M\rp\times P_{\overline M}(C) \\[0.3cm]
&= 0,1\times 0,3 + 0,9 \times 0,08 = 0,03 + 0,072 = 0,102\enar](/Generateur-Devoirs/TS/ChapProbabilites/ex113.AmeriqueSud_c/3.png)
-
- On choisit au hasard une victime d'un accident cardiaque.
La probabilité qu'elle présente une malformation cardiaque de type anévrisme est
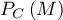 :
:
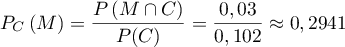
Partie B
- On peut considérer que, choisir au hasard un échantillon de 400 personnes, peut être assimilé à un tirage avec remise de 400 personnes dans la population totale.
Or la probabilité qu'une personne souffre d'une malformation cardiaque de type anévrisme est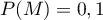 d'après l'énoncé.
d'après l'énoncé.
Donc on peut dire que la variable aléatoire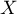 qui donne le nombre de personnes souffrant de cette malformation cardiaque suit une loi binomiale de paramètres
qui donne le nombre de personnes souffrant de cette malformation cardiaque suit une loi binomiale de paramètres 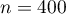 et
et 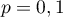 .
.
- Comme
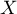 suit la loi binomiale
suit la loi binomiale 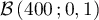 ,
,
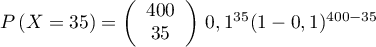 ;
;
le résultat donné par la calculatrice est approximativement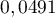 .
.
- La probabilité que
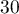 personnes de ce groupe, au moins,
présentent une malformation cardiaque de type anévrisme est
personnes de ce groupe, au moins,
présentent une malformation cardiaque de type anévrisme est
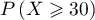 qui est égale à
qui est égale à 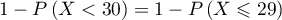 .
.
D'après la calculatrice,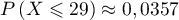 ,
donc
,
donc 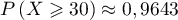 .
.
Partie C
- On sait que si
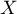 suit la loi binomiale
suit la loi binomiale 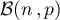 , alors l'intervalle de fluctuation asymptotique de la variable aléatoire
, alors l'intervalle de fluctuation asymptotique de la variable aléatoire 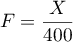 au seuil de
au seuil de 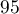 % est donné par:
% est donné par:
![\begin{array}{ll}
I&=\left[ p-1,96\dfrac{\sqrt{p(1-p)}}{\sqrt n}\,;\,p+1,96\dfrac{\sqrt{p(1-p)}}{\sqrt n}\rb\\[0.6cm]
&=\left[ 0,1-1,96\dfrac{\sqrt{0,1(1-0,1)}}{\sqrt{400}}\,;\,0,1+1,96\dfrac{\sqrt{0,1(1-0,1)}}{\sqrt{400}}\rb\\[0.6cm]
&=\Bigl[ 0,0706\,;\, 0,1294\Bigr]
\enar](/Generateur-Devoirs/TS/ChapProbabilites/ex113.AmeriqueSud_c/23.png)
- Dans l'échantillon considéré,
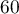 personnes présentent une malformation cardiaque de type anévrisme;
personnes présentent une malformation cardiaque de type anévrisme; 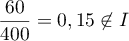 .
Le taux de malades dans cet échantillon est anormalement élevé.
.
Le taux de malades dans cet échantillon est anormalement élevé.
Cacher la correction
Exercice 3: Bac 2013 - Arbre, probabilités conditionnelles et loi binomiale
Bac S, 20 juin 2013, 4 points
Une jardinerie vend de jeunes plants d'arbres qui proviennent de trois horticulteurs : 35 % des plants proviennent de l'horticulteur , 25 % de l'horticulteur
, 25 % de l'horticulteur  et le reste de
l'horticulteur H
et le reste de
l'horticulteur H . Chaque horticulteur livre deux catégories
d'arbres : des conifères et des arbres à feuilles.
La livraison de l'horticulteur
. Chaque horticulteur livre deux catégories
d'arbres : des conifères et des arbres à feuilles.
La livraison de l'horticulteur  comporte 80 % de conifères alors que celle de l'horticulteur
comporte 80 % de conifères alors que celle de l'horticulteur  n'en comporte que 50 % et celle de l'horticulteur
n'en comporte que 50 % et celle de l'horticulteur  seulement 30 %.
seulement 30 %.
Puisque le choix de l'arbre se fait au hasard dans le stock de la jardinerie, on assimile les proportions données à des probabilités.
Cacher la correction
Une jardinerie vend de jeunes plants d'arbres qui proviennent de trois horticulteurs : 35 % des plants proviennent de l'horticulteur
- Le gérant de la jardinerie choisit un arbre au hasard dans son stock.
On envisage les événements suivants :
-
 : « l'arbre choisi a été acheté chez l'horticulteur H
: « l'arbre choisi a été acheté chez l'horticulteur H »,
»,
-
 : « l'arbre choisi a été acheté chez l'horticulteur H
: « l'arbre choisi a été acheté chez l'horticulteur H »,
»,
-
 : « l'arbre choisi a été acheté chez l'horticulteur H
: « l'arbre choisi a été acheté chez l'horticulteur H »,
»,
-
 : « l'arbre choisi est un conifère »,
: « l'arbre choisi est un conifère »,
-
 : « l'arbre choisi est un arbre feuillu ».
: « l'arbre choisi est un arbre feuillu ».
- Construire un arbre pondéré traduisant la situation.
- Calculer la probabilité que l'arbre choisi soit un conifère
acheté chez l'horticulteur
 .
.
- Justifier que la probabilité de l'évènement
 est égale à
est égale à  .
.
- L'arbre choisi est un conifère.
Quelle est la probabilité qu'il ait été acheté chez l'horticulteur
 ? On arrondira à
? On arrondira à  .
.
-
- On choisit au hasard un échantillon de
 arbres dans le stock
de cette jardinerie. On suppose que ce stock est suffisamment
important pour que ce choix puisse être assimilé à un tirage avec
remise de
arbres dans le stock
de cette jardinerie. On suppose que ce stock est suffisamment
important pour que ce choix puisse être assimilé à un tirage avec
remise de  arbres dans le stock.
On appelle
arbres dans le stock.
On appelle  la variable aléatoire qui donne le nombre de
conifères de l'échantillon choisi.
la variable aléatoire qui donne le nombre de
conifères de l'échantillon choisi.
- Justifier que
 suit une loi binomiale dont on
précisera les paramètres.
suit une loi binomiale dont on
précisera les paramètres.
- Quelle est la probabilité que l'échantillon prélevé comporte exactement
 conifères?
conifères?
On arrondira à .
.
- Quelle est la probabilité que cet échantillon comporte au moins deux arbres feuillus ?
On arrondira à
 .
.
- Justifier que
Correction exercice 3
Puisque le choix de l'arbre se fait au hasard dans le stock de la jardinerie, on assimile les proportions données à des probabilités.
-
- L'arbre pondéré traduisant cette situation est :

- On cherche la probabilité de l'intersection:
 .
.
- Puisque la jardinerie ne se fournit qu'auprès de trois
horticulteurs, les événements
 ,
,  et
et  forment une
partition de l'univers. On peut donc appliquer la loi des
probabilités totales, et on en déduit :
forment une
partition de l'univers. On peut donc appliquer la loi des
probabilités totales, et on en déduit :
 .
.
- On cherche cette fois à calculer une probabilité conditionnelle :
 .
.
- L'arbre pondéré traduisant cette situation est :
-
- On répète
 fois le schéma de Bernoulli pour lequel le
succès est "choisir un conifère", dont la probabilité est
fois le schéma de Bernoulli pour lequel le
succès est "choisir un conifère", dont la probabilité est
 .
Ces répétitions sont identiques et indépendantes (puisque l'on
suppose que les choix successifs peuvent être assimilés à un
tirage au sort avec remise).
.
Ces répétitions sont identiques et indépendantes (puisque l'on
suppose que les choix successifs peuvent être assimilés à un
tirage au sort avec remise).
Ainsi la variable aléatoire , égale au nombre de succès sur les
10 répétitions, suit bien la loi binomiale
, égale au nombre de succès sur les
10 répétitions, suit bien la loi binomiale  ,
soit ici
,
soit ici  .
.
- On cherche ici la probabilité de l'événement
 :
:
 .
.
- Cette fois, la probabilité recherchée est celle de
 , qui est l'événement contraire de la réunion des événements
disjoints
, qui est l'événement contraire de la réunion des événements
disjoints  et
et  .
.
On a alors: .
.
- On répète
Cacher la correction
Exercice 4: Bac 2016, Centre étrganers - Loi binomiale et probabilités conditionnelles pour un sondage
Un institut effectue un sondage pour connaître, dans une population donnée, la proportion de personnes qui sont favorables à un projet d'aménagement du territoire. Pour cela, on interroge un échantillon aléatoire de personnes de cette population, et l'on pose une question à chaque personne.
Les deux parties sont relatives à cette même situation, mais peuvent être traitées de manière indépendante.
Partie A : Nombre de personnes qui acceptent de répondre au sondage
On admet dans cette partie que la probabilité qu'une personne interrogée accepte de répondre à la question est égale à 0,6.
Partie B : Correction due à l'insincérité de certaines réponses
Dans cette partie, on suppose que, parmi les personnes sondées qui ont accepté de répondre à la question posée, 29% affirment qu'elles sont favorables au projet.
L'institut de sondage sait par ailleurs que la question posée pouvant être gênante pour les personnes interrogées, certaines d'entre elles ne sont pas sincères et répondent le contraire de leur opinion véritable. Ainsi, une personne qui se dit favorable peut :
Par expérience, l'institut estime à 15% le taux de réponses non sincères parmi les personnes ayant répondu, et admet que ce taux est le même quelle que soit l'opinion de la personne interrogée.
Le but de cette partie est, à partir de ces données, de déterminer le taux réel de personnes favorables au projet, à l'aide d'un modèle probabiliste. On prélève au hasard la fiche d'une personne ayant répondu, et on définit :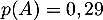 .
.
Partie A : Nombre de personnes qui acceptent de répondre au sondage
Partie B : Correction due à l'insincérité de certaines réponses
Cacher la correction
Les deux parties sont relatives à cette même situation, mais peuvent être traitées de manière indépendante.
Partie A : Nombre de personnes qui acceptent de répondre au sondage
On admet dans cette partie que la probabilité qu'une personne interrogée accepte de répondre à la question est égale à 0,6.
- L'institut de sondage interroge 700 personnes. On note
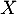 la variable aléatoire correspondant au nombre de personnes interrogées qui acceptent de répondre à la question posée.
la variable aléatoire correspondant au nombre de personnes interrogées qui acceptent de répondre à la question posée.
- Quelle est la loi de la variable aléatoire
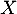 ? Justifier la réponse.
? Justifier la réponse.
- Quelle est la meilleure approximation de
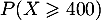 parmi les nombres suivants ?
parmi les nombres suivants ?
![\[0,92\hspace{2cm} 0,93\hspace{2cm}0,94\hspace{2cm}0,95.\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2016-CE/4.png)
- Quelle est la loi de la variable aléatoire
- Combien de personnes l'institut doit-il interroger au minimum pour garantir, avec une probabilité supérieure à 0,9, que le nombre de personnes répondant au sondage soit supérieur ou égal à 400.
Partie B : Correction due à l'insincérité de certaines réponses
Dans cette partie, on suppose que, parmi les personnes sondées qui ont accepté de répondre à la question posée, 29% affirment qu'elles sont favorables au projet.
L'institut de sondage sait par ailleurs que la question posée pouvant être gênante pour les personnes interrogées, certaines d'entre elles ne sont pas sincères et répondent le contraire de leur opinion véritable. Ainsi, une personne qui se dit favorable peut :
- soit être en réalité favorable au projet si elle est sincère.
- soit être en réalité défavorable au projet si elle n'est pas sincère.
Par expérience, l'institut estime à 15% le taux de réponses non sincères parmi les personnes ayant répondu, et admet que ce taux est le même quelle que soit l'opinion de la personne interrogée.
Le but de cette partie est, à partir de ces données, de déterminer le taux réel de personnes favorables au projet, à l'aide d'un modèle probabiliste. On prélève au hasard la fiche d'une personne ayant répondu, et on définit :
-
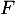 l'évènement « la personne est en réalité favorable au projet» ;
l'évènement « la personne est en réalité favorable au projet» ;
-
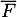 l'évènement « la personne est en réalité défavorable au projet» ;
l'évènement « la personne est en réalité défavorable au projet» ;
-
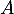 l'évènement « la personne affirme qu'elle est favorable au projet»;
l'évènement « la personne affirme qu'elle est favorable au projet»;
-
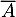 l'évènement « la personne affirme qu'elle est défavorable au projet».
l'évènement « la personne affirme qu'elle est défavorable au projet».
- En interprétant les données de l'énoncé, indiquer les valeurs de
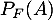 et
et 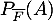 .
.
- On pose
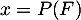 .
.
- Reproduire sur la copie et compléter l'arbre de probabilité ci-contre.
- En déduire une égalité vérifiée par
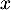
![\[\psset{xunit=1.4cm,yunit=0.5cm}
\begin{pspicture}(2,-3)(3,10)
\psline(1.5,-1.5)(0,0)(1.5,1.5)\rput(1.75,1.5){$F$}\rput(0.8,1.2){$x$}
\rput(1.75,-1.5){$\overline{F}$}\rput(0.8,-1.4){$1-x$}
\psline(3.5,0.5)(2,1.5)(3.5,3.)\rput(3.75,3){$A$}
\rput(3.75,0.5){$\overline{A}$}
\psline(3.5,-0.5)(2,-1.5)(3.5,-3.)\rput(3.75,-3){$\overline{A}$}
\rput(3.75,-0.5){$A$}
\end{pspicture} \]](/Generateur-Devoirs/TS/ChapProbabilites/ex2016-CE/14.png)
- Reproduire sur la copie et compléter l'arbre de probabilité ci-contre.
- Déterminer, parmi les personnes ayant répondu au sondage, la proportion de celles qui sont réellement favorables au projet.
Correction exercice 4
Partie A : Nombre de personnes qui acceptent de répondre au sondage
-
- On répète
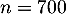 fois l'expérience aléatoire
"interroger une personne" dont le succès est "la personne accepte de répondre",
de probabilité
fois l'expérience aléatoire
"interroger une personne" dont le succès est "la personne accepte de répondre",
de probabilité 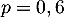 .
On peut supposer ces répétitions identiques et indépendantes.
La variable aléatoire
.
On peut supposer ces répétitions identiques et indépendantes.
La variable aléatoire 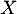 égale au nombre de succès, c'est-à-dire au
nombre de personnes qui acceptent de répondre, suit alors la loi binomiale
égale au nombre de succès, c'est-à-dire au
nombre de personnes qui acceptent de répondre, suit alors la loi binomiale
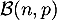 de paramètres
de paramètres 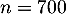 et
et 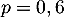 .
.
- Avec une calculatrice, on trouve que la meilleure approximation est
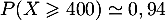
- On répète
- On cherche
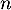 tel que
tel que 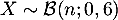 et
et
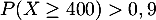 .
.
On trouve, avec la calculatrice,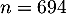 au minimum.
au minimum.
Partie B : Correction due à l'insincérité de certaines réponses
- L'énoncé donne les deux probabilités conditionnelles:
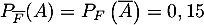 .
.
On en déduit aussi que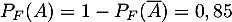 .
.
-
-
![\[\psset{xunit=1.4cm,yunit=0.6cm}
\begin{pspicture}(0,-3)(3,3)
\psline(1.5,-1.5)(0,0)(1.5,1.5)\rput(1.75,1.5){$F$}\rput(0.8,1.2){$x$}
\rput(1.75,-1.5){$\overline{F}$}\rput(0.8,-1.3){$1-x$}
\psline(3.5,0.5)(2,1.5)(3.5,3.)\rput(3.75,3){$A$}\rput(2.7,2.7){$0,85$}
\rput(3.75,0.5){$\overline{A}$}\rput(2.7,.6){$0,15$}
\psline(3.5,-0.5)(2,-1.5)(3.5,-3.)\rput(3.75,-3){$\overline{A}$}
\rput(2.7,-2.7){$0,85$}\rput(3.75,-0.5){$A$}
\rput(2.7,-.6){$0,15$} \end{pspicture} \]](/Generateur-Devoirs/TS/ChapProbabilites/ex2016-CE_c/14.png)
- On en déduit que
![\[P(A)=0,29=0,85x+0,15(1-x)\iff 0,7x=0,14 \iff x=0,2\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2016-CE_c/15.png)
-
- On en déduit que parmi les personnes ayant répondu,
20% sont réellement favorables au projet.
Cacher la correction
Exercice 5: Bac 2021, sujet 0 - Arbre pondéré, loi binomiale et python
Pour préparer l’examen du permis de conduire, on distingue deux types de formation :
On considère un groupe de 300 personnes venant de réussir l’examen du permis de conduire. Dans ce groupe :
On interroge au hasard une personne du groupe considéré.
On considère les évènements suivants :
Cacher la correction
- la formation avec conduite accompagnée ;
- la formation traditionnelle.
On considère un groupe de 300 personnes venant de réussir l’examen du permis de conduire. Dans ce groupe :
- 75 personnes ont suivi une formation avec conduite accompagnée ; parmi elles, 50 ont réussi l’examen à leur première présentation et les autres ont réussi à leur deuxième présentation.
- 225 personnes se sont présentées à l’examen suite à une formation traditionnelle ; parmi elles, 100 ont réussi l’examen à la première présentation, 75 à la deuxième et 50 à la troisième présentation.
On interroge au hasard une personne du groupe considéré.
On considère les évènements suivants :
-
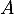 : « la personne a suivi une formation avec conduite accompagnée » ;
: « la personne a suivi une formation avec conduite accompagnée » ;
-
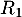 : « la personne a réussi l’examen à la première présentation » ;
: « la personne a réussi l’examen à la première présentation » ;
-
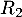 : « la personne a réussi l’examen à la deuxième présentation » ;
: « la personne a réussi l’examen à la deuxième présentation » ;
-
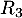 : « la personne a réussi l’examen à la troisième présentation ».
: « la personne a réussi l’examen à la troisième présentation ».
- Modéliser la situation par un arbre pondéré.
Dans les questions suivantes, les probabilités demandées seront données sous forme d’une fraction irréductible.
-
- Calculer la probabilité que la personne interrogée ait suivi une formation avec conduite accompagnée et réussi l’examen à sa deuxième présentation.
- Montrer que la probabilité que la personne interrogée ait réussi l’examen à sa deuxième présentation est égale à
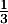 .
.
- La personne interrogée a réussi l’examen à sa deuxième présentation. Quelle est la probabilité qu’elle ait suivi une formation avec conduite accompagnée?
- On note
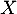 la variable aléatoire qui, à toute personne choisie au hasard dans le groupe, associe le nombre de fois où elle s’est présentée à l’examen jusqu’à sa réussite.
la variable aléatoire qui, à toute personne choisie au hasard dans le groupe, associe le nombre de fois où elle s’est présentée à l’examen jusqu’à sa réussite.
Ainsi,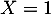 correspond à l’évènement
correspond à l’évènement 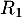 .
.
- Déterminer la loi de probabilité de la variable aléatoire
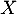 .
.
- Calculer l’espérance de cette variable aléatoire. Interpréter cette valeur dans le contexte de l’exercice.
- Déterminer la loi de probabilité de la variable aléatoire
- On choisit, successivement et de façon indépendante,
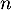 personnes parmi les 300 du groupe étudié, où
personnes parmi les 300 du groupe étudié, où 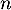 est un entier naturel non nul. On assimile ce choix à un tirage avec remise de
est un entier naturel non nul. On assimile ce choix à un tirage avec remise de 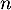 personnes parmi les 300 personnes du groupe.
On admet que la probabilité de l’évènement
personnes parmi les 300 personnes du groupe.
On admet que la probabilité de l’évènement 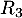 est égale à
est égale à 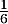 .
.
- Dans le contexte de cette question, préciser un évènement dont la probabilité est égale à
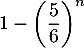 .
On considère la fonction Python seuil ci-dessous, où
.
On considère la fonction Python seuil ci-dessous, où 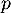 est un nombre réel appartenant à l’intervalle ]0;1[.
est un nombre réel appartenant à l’intervalle ]0;1[.
![\[\begin{tabular}[]{|l|}
\hline
\textbf{def seuil}(p):\\
\hspace{2em}n = 1\\
\hspace{2em}\textbf{while} 1$-$(5/6)**n $< =$ p:\\
\hspace{4.5em}n = n+1\\
\hspace{2em}\textbf{return} n\\
\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-sujet-0/17.png)
- Quelle est la valeur renvoyée par la commande seuil(0,9) ? Interpréter cette valeur dans le contexte de l’exercice.
- Dans le contexte de cette question, préciser un évènement dont la probabilité est égale à
Correction exercice 5
- On modélise la situation par un arbre pondéré.
{.3}\rput(3.3,1.6){$\frac{25}{75}$}
\rput(4.3,.5){$R_3$}\rput(3.3,.7){$0$}
%
\psline(2.5,-1.5)(4,-1.5)
\psline(4,-.5)(2.5,-1.5)(4,-2.5)
\rput(4.3,-.5){$R_1$}\rput(3.3,-.5){$\frac{100}{225}$}
\rput(4.3,-1.5){$R_2$}\pscircle[linestyle=none,fillstyle=solid,fillcolor=white](3.3,-1.6){.3}\rput(3.3,-1.5){$\frac{75}{225}$}
\rput(4.3,-2.5){$R_3$}\rput(3.3,-2.4){$\frac{50}{225}$}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-sujet-0_c/1.png)
-
- La probabilité que la personne interrogée ait suivi une formation avec conduite accompagnée et réussi l'examen à sa deuxième présentation est:
![\[\begin{array}{ll}P\left( A\cap R_2\rp&= P(A)\times P_{A}\left( R_2\rp\\[.3em]
&=\dfrac{75}{300}\tm\dfrac{25}{75}=\dfrac{1}{12}\enar\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-sujet-0_c/2.png)
- La probabilité que la personne interrogée ait réussi l'examen à sa deuxième présentation est
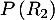 soit, d'après la formule des probabilités totales,
soit, d'après la formule des probabilités totales,
![\[\begin{array}{ll}
P\left( R_2\right) %&= P\left( A\cap R_2\right) + P\left(\overline{A}\cap R_2\right)\\
&= P_A\left( R_2\rp\times P(A) + P_{\overline{A}}\left( R_2\rp\times P\left(\overline{A}\rp\\[.3em]
&=\dfrac{75}{300}\tm\dfrac{25}{75}
+\dfrac{225}{300}\tm\dfrac{75}{225}\\[.7em]
&=\dfrac{25}{300} + \dfrac{75}{300}
=\dfrac{100}{300}=\dfrac13\enar\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-sujet-0_c/4.png)
- La personne interrogée a réussi l'examen à sa deuxième présentation. La probabilité qu'elle ait suivi une formation avec conduite accompagnée est alors la probabilité conditionnelle:
![\[P_{R_2}(A) = \dfrac{P\left (A\cap R_2 \right )}{P\left (R_2\right )}= \dfrac{\frac{1}{12}}{\frac{1}{3}} = \dfrac{3}{12}=\dfrac{1}{4}
\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-sujet-0_c/5.png)
- La probabilité que la personne interrogée ait suivi une formation avec conduite accompagnée et réussi l'examen à sa deuxième présentation est:
- On note
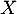 la variable aléatoire qui, à toute personne choisie au hasard dans le groupe, associe le nombre de fois où elle s'est présentée à l'examen jusqu'à sa réussite.
la variable aléatoire qui, à toute personne choisie au hasard dans le groupe, associe le nombre de fois où elle s'est présentée à l'examen jusqu'à sa réussite.
- La loi de probabilité de la variable aléatoire
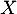 est:
est:
![\[\begin{tabular}{|*4{c|}}
\hline
$x_i$ & 1 & 2 & 3\\
\hline
$p_i=P(X=x_i)$ & $P(R_1)$ & $P(R_2)$ & $P(R_3)$ \\
\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-sujet-0_c/8.png)
soit, en calculant les différentes probabilités:
Donc la loi de probabilité de la variable aléatoire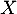 est:
est:
![\[\begin{tabular}{|*4{c|}}
\hline
$x_i$ & 1 & 2 & 3\\
\hline
$p_i=P(X=x_i)$ & $\dfrac{1}{2}$ & $\dfrac{1}{3}$ & $\dfrac{1}{6}$\rule[-10pt]{0pt}{28pt} \\
\hline
\end{tabular}\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-sujet-0_c/13.png)
-
- L'espérance de cette variable aléatoire est:
![\[\begin{array}{ll}E(X)&=\dsp\sum_{i=1}^3 x_i\times p_i\\&= 1\times\dfrac{1}{2} + 2 \times \dfrac{1}{3} + 3\times \dfrac{1}{6} \\
&= \dfrac{5}{3}\approx 1,67\enar\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-sujet-0_c/14.png)
Cela signifie que le nombre de passages pour réussir l'examen est en moyenne de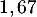 .
.
- La loi de probabilité de la variable aléatoire
- On choisit, successivement et de façon indépendante,
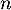 personnes parmi les 300 du groupe étudié, où
personnes parmi les 300 du groupe étudié, où 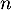 est un entier naturel non nul. On assimile ce choix à un tirage avec remise de
est un entier naturel non nul. On assimile ce choix à un tirage avec remise de 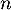 personnes parmi les 300 personnes du groupe.
personnes parmi les 300 personnes du groupe.
On admet que la probabilité de l'évènement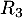 est égale à
est égale à 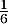 .
.
- On cherche un évènement dont la probabilité est égale à
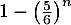 .
.
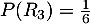 donc
donc 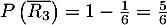 .
Le nombre
.
Le nombre 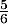 est donc la probabilité de l'événement "
est donc la probabilité de l'événement "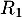 ou
ou 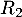 ", c'est-à-dire la probabilité qu'une personne prise au hasard réussisse l'examen à la première tentative ou à la deuxième.
", c'est-à-dire la probabilité qu'une personne prise au hasard réussisse l'examen à la première tentative ou à la deuxième.
La probabilité que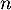 personnes réussissent l'examen à la première ou à la deuxième tentative est de
personnes réussissent l'examen à la première ou à la deuxième tentative est de 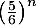 .
.
L'événement de probabilité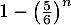 est l'événement contraire du précédent, donc correspond à l'événement "au moins une personne n'a pas réussi l'examen à la première ou à la deuxième tentative", c'est-à-dire "au moins une personne a réussi l'examen à la troisième tentative''.
est l'événement contraire du précédent, donc correspond à l'événement "au moins une personne n'a pas réussi l'examen à la première ou à la deuxième tentative", c'est-à-dire "au moins une personne a réussi l'examen à la troisième tentative''.
- La valeur renvoyée par seuil(0.9) est la première valeur de
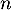 pour laquelle
pour laquelle 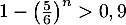 .
.
On résout cette inéquation:
![\[\begin{array}{ll}1-\lp\dfrac56\rp^n >0,9
&\iff
\lp\dfrac56\rp^n<0,1 \\[1em]
&\iff
\ln\lp\lp\dfrac56\rp^n\rp<\ln(0,1)\\[1em]
&\iff
n\ln\lp\dfrac56\rp<\ln(0,1)\\[1em]
&\iff
n<\dfrac{\ln(0,1)}{\ln\lp\dfrac56\right)}\sim12,6
\enar\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-sujet-0_c/32.png)
La commande seuil(0.9) renvoie donc la valeur 13.
Il faut donc prendre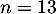 personnes sur les 300 pour que la probabilité d'en avoir une qui a réussi l'examen à sa troisième tentative soit supérieure à
personnes sur les 300 pour que la probabilité d'en avoir une qui a réussi l'examen à sa troisième tentative soit supérieure à 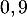 .
.
- On cherche un évènement dont la probabilité est égale à
Cacher la correction
Exercice 6: Bac 2021 - Arbre pondéré, probabilités conditionnelles et loi binomiale: recrutement dans une école
Dans une école de statistique, après étude des dossiers des candidats,
le recrutement se fait de deux façons :
On choisit au hasard un candidat à ce concours de recrutement. On notera:
Partie 2
Bac 2021 - 15 mars, sujet 1
Partie 1
Partie 2
Cacher la correction
- 10 % des candidats sont sélectionnés sur dossier. Ces candidats doivent ensuite passer un oral à l'issue duquel 60 % d'entre eux sont finalement admis à l'école.
- Les candidats n'ayant pas été sélectionnés sur dossier passent une épreuve écrite à l'issue de laquelle 20 % d'entre eux sont admis à l'école.
On choisit au hasard un candidat à ce concours de recrutement. On notera:
-
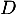 l'évènement « le candidat a été sélectionné sur dossier »;
l'évènement « le candidat a été sélectionné sur dossier »;
-
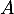 l'évènement « le candidat a été admis à l'école »;
l'évènement « le candidat a été admis à l'école »;
-
 et
et  les évènements contraires des évènements
les évènements contraires des évènements 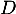 et
et 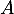 respectivement.
respectivement.
- Traduire la situation par un arbre pondéré.
- Calculer la probabilité que le candidat soit sélectionné sur dossier et admis à l'école.
- Montrer que la probabilité de l'évènement
 est égale à
est égale à  .
.
- On choisit au hasard un candidat admis à l'école. Quelle est la probabilité que son dossier n'ait pas été sélectionné?
Partie 2
- On admet que la probabilité pour un candidat d'être admis à l'école est égale à
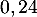 .
.
On considère un échantillon de sept candidats choisis au hasard, en assimilant ce choix à un tirage au sort avec remise. On désigne par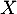 la variable aléatoire dénombrant les candidats admis à l'école parmi les sept tirés au sort.
la variable aléatoire dénombrant les candidats admis à l'école parmi les sept tirés au sort.
- On admet que la variable aléatoire
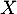 suit une loi binomiale. Quels sont les paramètres de cette loi?
suit une loi binomiale. Quels sont les paramètres de cette loi?
- Calculer la probabilité qu'un seul des sept candidats tirés au sort soit admis à l'école. On donnera une réponse arrondie au centième.
- Calculer la probabilité qu'au moins deux des sept candidats tirés au sort soient admis à cette école. On donnera une réponse arrondie au centième.
- On admet que la variable aléatoire
- Un lycée présente
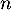 candidats au recrutement dans cette école, où
candidats au recrutement dans cette école, où 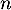 est un entier naturel non nul.
est un entier naturel non nul.
On admet que la probabilité pour un candidat quelconque du lycée d'être admis à l'école est égale à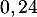 et que les résultats des candidats sont indépendants les uns des autres.
et que les résultats des candidats sont indépendants les uns des autres.
- Donner l'expression, en fonction de
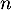 , de la probabilité qu'aucun candidat issu de ce lycée ne soit admis à l'école.
, de la probabilité qu'aucun candidat issu de ce lycée ne soit admis à l'école.
- À partir de quelle valeur de l'entier
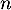 la probabilité qu'au moins un élève de ce lycée soit admis à l'école est-elle supérieure ou égale à
la probabilité qu'au moins un élève de ce lycée soit admis à l'école est-elle supérieure ou égale à 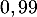 ?
?
- Donner l'expression, en fonction de
Correction exercice 6
Bac 2021 - 15 mars, sujet 1
Partie 1
-
![\[\psset{xunit=1.3cm,yunit=.8cm}
\begin{pspicture}(-.4,-2)(4.2,2)
%\rput(0,0){$A_1$}
\psline(0,0)(1.5,1)\rput(1.75,1){$D$}
\rput(.8,.9){0,1}
\rput(.8,-1){0,9}
\psline(0,0)(1.5,-1)\rput(1.75,-1){$\overline{D}$}
\psline(2.1,1.2)(3.5,1.6)\rput(3.8,1.6){$A$}
\rput(2.8,1.7){0,6}
\psline(2.1,.8)(3.5,.4)\rput(3.8,.4){$\overline{A}$}
\rput(2.8,.2){0,4}
\rput(2.8,-.4){0,2}
\psline(2.1,-1.2)(3.5,-1.6)\rput(3.8,-1.6){$\overline{A}$}
\psline(2.1,-.8)(3.5,-.4)\rput(3.8,-.4){$A$}
\rput(2.8,-1.8){0,8}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-sujet-1_c/1.png)
- La probabilité que le candidat soit sélectionné sur dossier et admis à l'école est:
![\[P(D\cap A)=0,1\tm0,6=0,06\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-sujet-1_c/2.png)
- La probabilité de l'évènement
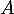 est,
d'après la formule des probabilités totales:
est,
d'après la formule des probabilités totales:
![\[\begin{array}{ll}P(A)
&= P(D\cap A) + P(\overline{D}\cap A) \\
&= 0,06 + 0,9\times 0,2 = 0,24\enar\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-sujet-1_c/4.png)
- La probabilité que le dossier n'ait pas été sélectionné,
sachant qu'il a été admis à l'école, est
![\[P_A(\overline{D})
=\dfrac{P(\overline{D}\cap A)}{P(A)}
=\dfrac{0,18}{0,24}=0,75\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-sujet-1_c/5.png)
Partie 2
-
- La probabilité du succés, un candidat d'être admis à l'école,
est
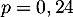 , et on choisit un échantillon de
, et on choisit un échantillon de  candidats.
candidats.
La variable aléatoire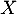 suit donc la loi binomiale
suit donc la loi binomiale
 .
.
- La probabilité qu'un seul des sept candidats tirés au sort soit admis à l'école est:
![\[P(X=1)=\binom{7}{1}\times 0,24^1 \times (1-0,24)^{7-1} \approx 0,32\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-sujet-1_c/10.png)
- La probabilité qu'au moins deux des sept candidats tirés au sort
soient admis à cette école est:
![\[P(X\geqslant 2) = 1-P(X\leqslant 1) = 1-0,47=0,53\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-sujet-1_c/11.png)
- La probabilité du succés, un candidat d'être admis à l'école,
est
-
- La variable aléatoire
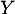 qui donne le nombre d'admis
parmi les
qui donne le nombre d'admis
parmi les 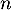 candidats présentés suit la loi binomiale
candidats présentés suit la loi binomiale
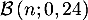 .
La probabilité qu'aucun candidat issu de ce lycée ne soit admis
à l'école est donc
.
La probabilité qu'aucun candidat issu de ce lycée ne soit admis
à l'école est donc
![\[P(Y=0)=\binom{n}{0}\times 0,24^0 \times 0,76^n=0,76^n\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-sujet-1_c/15.png)
- On cherche à partir de quelle valeur de l'entier
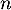 la probabilité
qu'au moins un élève de ce lycée soit admis à l'école est supérieure
ou égale à
la probabilité
qu'au moins un élève de ce lycée soit admis à l'école est supérieure
ou égale à 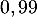 ,
,
![\[\begin{array}{ll}P(Y\geqslant 1) \geqslant 0,99 &\iff 1-P(Y=0) \geqslant 0,99\\
&\iff P(Y=0) \leqslant 0,01\\
&\iff 0,76^n \leqslant 0,01\\
&\iff \ln\left( 0,76^n\right) \leqslant \ln(0,01)\\
&\iff n \times \ln(0,76) \leqslant \ln(0,01)\\
&\iff n \geqslant \dfrac{\ln(0,01)}{\ln(0,76)}\simeq16,8
\enar\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-sujet-1_c/18.png)
car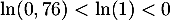 .
.
On trouve donc qu'à partir de 17 élèves la probabilité qu'au moins un élève de ce lycée soit admis à l'école est supérieure ou égale à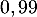 .
.
- La variable aléatoire
Cacher la correction
Exercice 7: Bac 2021, Centres étrangers - Arbre pondéré et loi binomiale: sondage l'utilisation des transports en commun
Dans tout cet exercice, les probabilités seront arrondies, si nécessaire, à  .
.
D'après une étude, les utilisateurs réguliers de transports en commun représentent 17 % de la population française.
Parmi ces utilisateurs réguliers, 32 % sont des jeunes âgés de 18 à 24 ans. (Source : TNS-Sofres)
Partie A :
On interroge une personne au hasard et on note :
Partie B :
Lors d'un recensement sur la population française, un recenseur interroge au hasard 50 personnes en une journée sur leur pratique des transports en commun.
La population française est suffisamment importante pour assimiler ce recensement à un tirage avec remise.
Soit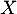 la variable aléatoire dénombrant les personnes utilisant régulièrement les transports en commun parmi les 50 personnes interrogées.
la variable aléatoire dénombrant les personnes utilisant régulièrement les transports en commun parmi les 50 personnes interrogées.
Bac centres étrangers, 9 juin 2021
Partie A.
Partie B.
Cacher la correction
D'après une étude, les utilisateurs réguliers de transports en commun représentent 17 % de la population française.
Parmi ces utilisateurs réguliers, 32 % sont des jeunes âgés de 18 à 24 ans. (Source : TNS-Sofres)
Partie A :
On interroge une personne au hasard et on note :
-
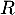 l'évènement : « La personne interrogée utilise régulièrement les transports en commun ».
l'évènement : « La personne interrogée utilise régulièrement les transports en commun ».
-
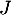 l'évènement : « La personne interrogée est âgée de 18 à 24 ans ».
l'évènement : « La personne interrogée est âgée de 18 à 24 ans ».
- Représentez la situation à l'aide de cet arbre pondéré, que vous recopierez sur votre copie, en y reportant les données de l'énoncé.
![\[\psset{xunit=1.3cm,yunit=1cm}
\begin{pspicture}(-.4,-2)(4.2,2)
%\rput(0,0){$A_1$}
\psline(0,0)(1.5,1)\rput(1.75,1){$R$}
\psline(0,0)(1.5,-1)\rput(1.75,-1){$\overline{R}$}
\psline(2.1,1.2)(3.5,1.6)\rput(3.8,1.6){$J$}
\psline(2.1,.8)(3.5,.4)\rput(3.8,.4){$\overline{J}$}
\psline(2.1,-1.2)(3.5,-1.6)\rput(3.8,-1.6){$\overline{J}$}
\psline(2.1,-.8)(3.5,-.4)\rput(3.8,-.4){$J$}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-CE/4.png)
- Calculer la probabilité
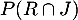 .
.
- D'après cette même étude, les jeunes de 18 à 24 ans représentent 11 % de la population française.
Montrer que la probabilité que la personne interrogée soit un jeune de 18 à 24 ans n'utilisant pas régulièrement les transports en commun est 0,056 à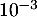 près.
près.
- En déduire la proportion de jeunes de 18 à 24 ans parmi les utilisateurs non réguliers des transports en commun.
Partie B :
Lors d'un recensement sur la population française, un recenseur interroge au hasard 50 personnes en une journée sur leur pratique des transports en commun.
La population française est suffisamment importante pour assimiler ce recensement à un tirage avec remise.
Soit
- Déterminer, en justifiant, la loi de
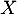 et préciser ses paramètres.
et préciser ses paramètres.
- Calculer
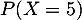 et interpréter le résultat.
et interpréter le résultat.
- Le recenseur indique qu'il y a plus de 95 % de chance pour que, parmi les
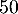 personnes interrogées, moins de
personnes interrogées, moins de 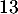 d'entre elles utilisent régulièrement les transports en commun.
d'entre elles utilisent régulièrement les transports en commun.
Cette affirmation est-elle vraie ? Justifier votre réponse. - Quel est le nombre moyen de personnes utilisant régulièrement les transports en commun parmi les
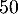 personnes interrogées ?
personnes interrogées ?
Correction exercice 7
Bac centres étrangers, 9 juin 2021
Partie A.
-
![\[\psset{xunit=1.3cm,yunit=.8cm}
\begin{pspicture}(-.4,-2)(4.2,2)
%\rput(0,0){$A_1$}
\psline(0,0)(1.5,1)\rput(1.75,1){$R$}
\rput(.8,.9){17\%}
\psline(0,0)(1.5,-1)\rput(1.75,-1){$\overline{R}$}
\psline(2.1,1.2)(3.5,1.6)\rput(3.8,1.6){$J$}
\rput(2.8,1.7){32\%}
\psline(2.1,.8)(3.5,.4)\rput(3.8,.4){$\overline{J}$}
\psline(2.1,-1.2)(3.5,-1.6)\rput(3.8,-1.6){$\overline{J}$}
\psline(2.1,-.8)(3.5,-.4)\rput(3.8,-.4){$J$}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-CE_c/1.png)
-
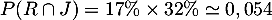
- On sait donc de plus que
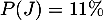 et on cherche
et on cherche
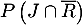 .
.
On a donc, d'après la formule des probabilités totales,
![\[P(J)=P(J\cap R)+P(J\cap\overline{R})\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-CE_c/5.png)
d'où
![\[P\left( J\cap\overline{R}\rp=P(J)-P(J\cap R)
\simeq11\%-0,054=0,056\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-CE_c/6.png)
- On cherche cette fois la probabilité conditionnelle
![\[P_{\overline{R}}(J)
=\dfrac{P\left( J\cap \overline{R}\right)}{P\left(\overline{R}\right)}
\simeq\dfrac{0,056}{1-0,17}\simeq0,067\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-CE_c/7.png)
Partie B.
- On répète
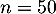 fois l'expérience aléatoire "interroger une personne sur ses pratiques des transports en commun", dont le succès est "la personne utilise régulièrement les transports en commun" de probabilité
fois l'expérience aléatoire "interroger une personne sur ses pratiques des transports en commun", dont le succès est "la personne utilise régulièrement les transports en commun" de probabilité 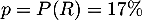 (de la partie A).
(de la partie A).
Ces répétitions sont supposées identiques et indépendantes.
On note enfin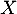 la variable aléatoire égale au nombre de succès,
c'est-à-dire au nombre de personnes sur ces 50 interrogées qui utilisent
régulièrement les transports en commun.
la variable aléatoire égale au nombre de succès,
c'est-à-dire au nombre de personnes sur ces 50 interrogées qui utilisent
régulièrement les transports en commun.
La variable aléatoire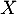 suit donc la loi binomiale
suit donc la loi binomiale
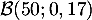 .
.
- On a donc, avec la calculatrice
![\[P(X=5)=\binom{50}{5}\tm0,17^5\tm0,83^{45}\simeq0,069\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-CE_c/13.png)
- On calcule la probablité correspondante, à l'aide de la calculatrice:
![\[P(X<13)=P(X\leq12)\simeq 0,93<0,95\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-CE_c/14.png)
ce qui indique que l'affirmation du recenseur est fause.
- Le nombre moyen est donné par l'espérance, soit ici
![\[E(X)=np=50\tm0,17=8,5\]](/Generateur-Devoirs/TS/ChapProbabilites/ex2021-CE_c/15.png)
Cacher la correction
Exercice 8: Bac 2022 - Arbre, loi binomiale et python
Le directeur d'une grande entreprise a proposé à l'ensemble de ses salariés un stage de formation à l'utilisation d'un nouveau logiciel.
Ce stage a été suivi par 25 % des salariés.
Cacher la correction
Ce stage a été suivi par 25 % des salariés.
- Dans cette entreprise, 52 % des salariés sont des femmes, parmi lesquelles
40 % ont suivi le stage.
On interroge au hasard un salarié de l'entreprise et on considère les évènements: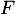 : « le salarié interrogé est une femme »,
: « le salarié interrogé est une femme »,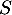 : « le salarié interrogé a suivi le stage ».
: « le salarié interrogé a suivi le stage ».
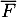 et
et  désignent respectivement les évènements contraires des évènements
désignent respectivement les évènements contraires des évènements  et
et  .
.
- Donner la probabilité de l'évènement

- Recopier et compléter les pointillés de l'arbre pondéré ci-contre sur
les quatre branches indiquées.
- Démontrer que la probabilité que la personne interrogée soit une femme ayant suivi le stage est égale à
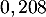 .
.
- On sait que la personne interrogée a suivi le stage. Quelle est la probabilité que ce soit une femme ?
- Le directeur affirme que, parmi les hommes salariés de l'entreprise, moins de 10 % ont suivi le stage. Justifier l'affirmation du directeur.
![\[\psset{xunit=1.3cm,yunit=1.4cm}
\begin{pspicture}(-.4,-2)(4.2,2)
\psline(0,0)(1.5,1)\rput(1.75,1){$F$}
\rput(.8,.9){\dots}
\rput(.8,-1){\dots}
\psline(0,0)(1.5,-1)\rput(1.75,-1){$\overline{F}$}
\psline(2.1,1.2)(3.5,1.6)\rput(3.8,1.6){$S$}
\rput(2.8,1.7){\dots}
\psline(2.1,.8)(3.5,.4)\rput(3.8,.4){$\overline{S}$}
\rput(2.8,.2){\dots}
%\rput(2.8,-.4){}
\psline(2.1,-1.2)(3.5,-1.6)\rput(3.8,-1.6){$\overline{S}$}
\psline(2.1,-.8)(3.5,-.4)\rput(3.8,-.4){$S$}
%\rput(2.8,-1.8){}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapProbabilites/ex11052022/11.png)
- On note
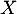 la variable aléatoire qui à un échantillon de
la variable aléatoire qui à un échantillon de 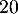 salariés de cette entreprise choisis au hasard associe le nombre de salariés de cet échantillon ayant suivi le stage. On suppose que l'effectif des salariés de l'entreprise est suffisamment important pour assimiler ce choix à un tirage avec remise.
salariés de cette entreprise choisis au hasard associe le nombre de salariés de cet échantillon ayant suivi le stage. On suppose que l'effectif des salariés de l'entreprise est suffisamment important pour assimiler ce choix à un tirage avec remise.
- Déterminer, en justifiant, la loi de probabilité suivie par la variable aléatoire X,
- Déterminer, à
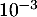 près, la probabilité que 5 salariés dans un échantillon de 20 aient suivi le stage.
près, la probabilité que 5 salariés dans un échantillon de 20 aient suivi le stage.
- Le programme ci-dessous, écrit en langage Python, utilise la fonction binomiale
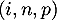 créée pour l'occasion qui renvoie
la valeur de la probabilité
créée pour l'occasion qui renvoie
la valeur de la probabilité 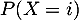 dans le cas où la variable aléatoire
dans le cas où la variable aléatoire 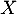 suit une loi binomiale de paramètres
suit une loi binomiale de paramètres 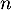 et
et 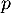 .
.
![\[\fbox{\begin{minipage}{7cm}
def proba(k):\\
\hspace*{2em} P=0\\
\hspace*{2em} for i in range(0,k+1) :\\
\hspace*{4em} P=P+binomiale(i,20,0.25)\\
\hspace*{2em} return P
\end{minipage}}\]](/Generateur-Devoirs/TS/ChapProbabilites/ex11052022/20.png)
Déterminer, à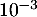 près, la valeur renvoyée par ce programme lorsque l'on saisit proba(5) dans la console Python.
Interpréter cette valeur dans le contexte de l'exercice.
près, la valeur renvoyée par ce programme lorsque l'on saisit proba(5) dans la console Python.
Interpréter cette valeur dans le contexte de l'exercice.
- Déterminer, à
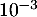 près, la probabilité qu'au moins 6 salariés dans un échantillon de 0 aient suivi le stage.
près, la probabilité qu'au moins 6 salariés dans un échantillon de 0 aient suivi le stage.
- Cette question est indépendante des questions 1 et 2.
Pour inciter les salariés à suivre le stage, l'entreprise avait décidé d'augmenter les salaires des salariés ayant suivi le stage de 5 %, contre 2 % d'augmentation pour les salariés n'ayant pas suivi le stage. Quel est le pourcentage moyen d'augmentation des salaires de cette entreprise dans ces conditions ?
Correction exercice 8
-
- D'après l'énoncé, on a
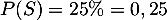 .
.
-
![\[\psset{xunit=1.3cm,yunit=1.4cm}
\begin{pspicture}(-.4,-2)(4.2,2)
\psline(0,0)(1.5,1)\rput(1.75,1){$F$}
\rput(.8,.9){52\%}
\rput(.8,-1){48\%}
\psline(0,0)(1.5,-1)\rput(1.75,-1){$\overline{F}$}
\psline(2.1,1.2)(3.5,1.6)\rput(3.8,1.6){$S$}
\rput(2.8,1.7){40\%}
\psline(2.1,.8)(3.5,.4)\rput(3.8,.4){$\overline{S}$}
\rput(2.8,.2){60\%}
%\rput(2.8,-.4){}
\psline(2.1,-1.2)(3.5,-1.6)\rput(3.8,-1.6){$\overline{S}$}
\psline(2.1,-.8)(3.5,-.4)\rput(3.8,-.4){$S$}
%\rput(2.8,-1.8){}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapProbabilites/ex11052022_c/2.png)
- On cherche la probablité
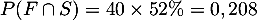 .
.
- La probabilité que ce soit une femme, sachant qu'elle a suivi le stage,
est la probabilité conditionnelle
![\[P_S(F)=\dfrac{P(S\cap F)}{P(S)}=\dfrac{0,208}{0,25}
=0,832\]](/Generateur-Devoirs/TS/ChapProbabilites/ex11052022_c/4.png)
- D'après l'arbre, ou la formule des probabilités totales,
on a
![\[P(S)=25\%=52\%\tm40\%+48\%\tm P_{\overline{F}}(S)\]](/Generateur-Devoirs/TS/ChapProbabilites/ex11052022_c/5.png)
et donc
![\[P_{\overline{F}}(S)=\dfrac{0,25-0.208}{0,48}=\]](/Generateur-Devoirs/TS/ChapProbabilites/ex11052022_c/6.png)
![\[=\dfrac{P(\overline{F}\cap S)}{P(\overline{F})}
=\dfrac{P(\overline{F}\cap S)}{48\%}=0,0875=8,75\%\]](/Generateur-Devoirs/TS/ChapProbabilites/ex11052022_c/7.png)
ce qui est en effet moins de 10% comme l'affirme le directeur.
- D'après l'énoncé, on a
- On note
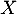 la variable aléatoire qui à un échantillon de
la variable aléatoire qui à un échantillon de  salariés de cette entreprise choisis au hasard associe le nombre de salariés de cet échantillon ayant suivi le stage. On suppose que l'effectif des salariés de l'entreprise est suffisamment important pour assimiler ce choix à un tirage avec remise.
salariés de cette entreprise choisis au hasard associe le nombre de salariés de cet échantillon ayant suivi le stage. On suppose que l'effectif des salariés de l'entreprise est suffisamment important pour assimiler ce choix à un tirage avec remise.
- Pour former un échantillon de 20 salariés, on répète
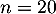 fois
l'expérience aléatoire "désigner au hasard un salarié" dont le succès est
"le salarié a suivi le stage" de probabilité
fois
l'expérience aléatoire "désigner au hasard un salarié" dont le succès est
"le salarié a suivi le stage" de probabilité 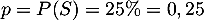 .
Cs répétitions sont supposées identiques et indépendantes car le tirage est assimilé à un tirage avec remise.
.
Cs répétitions sont supposées identiques et indépendantes car le tirage est assimilé à un tirage avec remise.
La variable aléatoire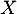 égale au nombre de scuccès, c'est-à-dire au nombre de salarié ayant suivi le stage dans l'échantillon suit donc la loi binomiale de paramètres
égale au nombre de scuccès, c'est-à-dire au nombre de salarié ayant suivi le stage dans l'échantillon suit donc la loi binomiale de paramètres 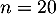 et
et 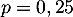 .
.
- À l'aide de la calculatrice, on trouve la probabilité
![\[P(X=5)\simeq 0,202\]](/Generateur-Devoirs/TS/ChapProbabilites/ex11052022_c/15.png)
- Ce programme calcule les probabilités cumulées, c'est-à-dire
![\[P(X\leqslant k)=P(X=0)+P(X=1)+\dots+P(X=k)\]](/Generateur-Devoirs/TS/ChapProbabilites/ex11052022_c/16.png)
Lorsque l'on saisit proba(5) dans la console Python, le porgramme retourne donc la valeur
![\[P(X\leqslant5)\simeq0,617\]](/Generateur-Devoirs/TS/ChapProbabilites/ex11052022_c/17.png)
Il s'agit de la probabilité que moins de 5 personnes aient suivi le stage dans l'échantillon de 20 personnes.
- La probabilité qu'au moins 6 salariés dans un échantillon de 20 aient suivi le stage est
![\[P(X\geqslant6)=1-P(X\leqslant5)\simeq 0,383\]](/Generateur-Devoirs/TS/ChapProbabilites/ex11052022_c/18.png)
- Pour former un échantillon de 20 salariés, on répète
- 25% des salariés ont suivi le stage et ont donc été augmentés de 5%,
les autres 75% ont été augmentés de 2%.
En moyenne, le pourventage d'augmentation est donc de
![\[25\%\tm5\%+75\%\tm2\%=2,75\%\]](/Generateur-Devoirs/TS/ChapProbabilites/ex11052022_c/19.png)
Cacher la correction
Exercice 9: Bac 2022 - Arbre et loi binomiale: test de dépistage pour les coyotes
Le coyote est un animal sauvage proche du loup, qui vit en Amérique du Nord.
Dans l'état d'Oklahoma, aux États-Unis, 70 % des coyotes sont touchés par une maladie appelée ehrlichiose.
Il existe un test aidant à la détection de cette maladie. Lorsque ce test est appliqué à un coyote, son résultat est soit positif, soit négatif, et on sait que :
Partie A
Des vétérinaires capturent un coyote d'Oklahoma au hasard et lui font subir un test pour l'ehrlichiose.
On considère les évènements suivants :
On note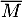 et
et 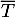 respectivement les évènements contraires de M et T.
respectivement les évènements contraires de M et T.
Partie B
On rappelle que la probabilité qu'un coyote capturé au hasard présente un test positif est de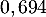 .
.
Partie A
Partie B
Cacher la correction
Dans l'état d'Oklahoma, aux États-Unis, 70 % des coyotes sont touchés par une maladie appelée ehrlichiose.
Il existe un test aidant à la détection de cette maladie. Lorsque ce test est appliqué à un coyote, son résultat est soit positif, soit négatif, et on sait que :
- Si le coyote est malade, le test est positif dans 97 % des cas.
- Si le coyote n'est pas malade, le test est négatif dans 95 % des cas.
Partie A
Des vétérinaires capturent un coyote d'Oklahoma au hasard et lui font subir un test pour l'ehrlichiose.
On considère les évènements suivants :
- M: « le coyote est malade »;
- T: « le test du coyote est positif ».
On note
- Recopier et compléter l'arbre pondéré ci-dessous qui modélise la situation.
![\[\psset{xunit=1.3cm,yunit=1.4cm}
\begin{pspicture}(-.4,-2)(4.2,2)
\psline(0,0)(1.5,1)\rput(1.75,1){$M$}
\rput(.8,.9){\dots}
\rput(.8,-1){\dots}
\psline(0,0)(1.5,-1)\rput(1.75,-1){$\overline{M}$}
\psline(2.1,1.2)(3.5,1.6)\rput(3.8,1.6){$T$}
\rput(2.8,1.7){\dots}
\psline(2.1,.8)(3.5,.4)\rput(3.8,.4){$\overline{T}$}
\rput(2.8,.2){\dots}
\rput(2.8,-.4){\dots}
\psline(2.1,-1.2)(3.5,-1.6)\rput(3.8,-1.6){$\overline{T}$}
\psline(2.1,-.8)(3.5,-.4)\rput(3.8,-.4){$T$}
\rput(2.8,-1.8){\dots}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapProbabilites/ex12052022/7.png)
- Déterminer la probabilité que le coyote soit malade et que son test soit positif.
- Démontrer que la probabilité de T est égale à
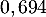 .
.
- On appelle « valeur prédictive positive du test » la probabilité que le coyote soit effectivement malade sachant que son test est positif.
Calculer la valeur prédictive positive du test. On arrondira le résultat au millième. -
- Par analogie avec la question précédente, proposer une définition de la « valeur prédictive négative du test » et calculer cette valeur en arrondissant au millième.
- Comparer les valeurs prédictives positive et négative du test, et interpréter.
Partie B
On rappelle que la probabilité qu'un coyote capturé au hasard présente un test positif est de
- Lorsqu'on capture au hasard cinq coyotes, on assimile ce choix à un tirage avec remise.
On note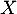 la variable aléatoire qui à un échantillon de cinq coyotes capturés au hasard associe le nombre de coyotes dans cet échantillon ayant un test positif.
la variable aléatoire qui à un échantillon de cinq coyotes capturés au hasard associe le nombre de coyotes dans cet échantillon ayant un test positif.
- Quelle est la loi de probabilité suivie par
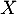 ? Justifier et préciser ses paramètres.
? Justifier et préciser ses paramètres.
- Calculer la probabilité que dans un échantillon de cinq coyotes capturés au hasard, un seul ait un test positif. On arrondira le résultat au centième.
- Un vétérinaire affirme qu'il y a plus d'une chance sur deux qu'au moins quatre coyotes sur cinq aient un test positif : cette affirmation est-elle vraie ? Justifier la réponse.
- Quelle est la loi de probabilité suivie par
- Pour tester des médicaments, les vétérinaires ont besoin de disposer d'un coyote présentant un test positif. Combien doivent-ils capturer de coyotes pour que la probabilité qu'au moins l'un d'entre eux présente un test positif soit supérieure à
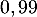 ?
?
Correction exercice 9
Partie A
-
![\[\psset{xunit=1.3cm,yunit=1.4cm}
\begin{pspicture}(-.4,-2)(4.2,2)
\psline(0,0)(1.5,1)\rput(1.75,1){$M$}
\rput(.8,.9){70\%}
\rput(.8,-1){30\%}
\psline(0,0)(1.5,-1)\rput(1.75,-1){$\overline{M}$}
\psline(2.1,1.2)(3.5,1.6)\rput(3.8,1.6){$T$}
\rput(2.8,1.7){97\%}
\psline(2.1,.8)(3.5,.4)\rput(3.8,.4){$\overline{T}$}
\rput(2.8,.4){3\%}
\rput(2.8,-.4){5\%}
\psline(2.1,-1.2)(3.5,-1.6)\rput(3.8,-1.6){$\overline{T}$}
\psline(2.1,-.8)(3.5,-.4)\rput(3.8,-.4){$T$}
\rput(2.8,-1.7){95\%}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapProbabilites/ex12052022_c/1.png)
- D'après l'arbre, la probabilité que le coyote soit malade
et que son test soit positif est
![\[P(\overline{M}\cap T)=30\%\tm5\%=1,5\%\]](/Generateur-Devoirs/TS/ChapProbabilites/ex12052022_c/2.png)
- D'après l'arbre, ou la formule des probabilités totales,
![\[P(T)=70\%\tm97\%+30\%\tm5\%=69,4\%=0,694\]](/Generateur-Devoirs/TS/ChapProbabilites/ex12052022_c/3.png)
- La valeur prédictive positive du test est la probabilité conditionnelle
![\[P_T(M)=\dfrac{P(M\cap T)}{P(T)}=\dfrac{70\%\tm97\%}{69,4\%}\simeq0,978=97,8\%\]](/Generateur-Devoirs/TS/ChapProbabilites/ex12052022_c/4.png)
-
- Par analogie avec la question précédente, la « valeur prédictive négative du test » est la probabilité que le coyote ne soit effectivement pas malade sachant que son test est négatif, et vaut
![\[P_{\overline{T}}(\overline{M})=\dfrac{P(\overline{T}\cap\overline{M})}{P(\overline{T})}
=\dfrac{30\%\tm95\%}{1-0,694}\simeq0,931=93,1\%\]](/Generateur-Devoirs/TS/ChapProbabilites/ex12052022_c/5.png)
- La valeur prédictive positive est plus grande que celle négative: le test est donc plus fiable pour diagonostiquer un animal malade qu'un animal sain.
- Par analogie avec la question précédente, la « valeur prédictive négative du test » est la probabilité que le coyote ne soit effectivement pas malade sachant que son test est négatif, et vaut
Partie B
-
- On répète
 fois l'expérience aléatoire "capturer un coyote",
dont le succès est "le coyote a un test positif" de probabilité
fois l'expérience aléatoire "capturer un coyote",
dont le succès est "le coyote a un test positif" de probabilité
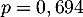 .
Ces répétitions sont identiques et indépendantes (car on l'assimile à un tirage avec remise).
.
Ces répétitions sont identiques et indépendantes (car on l'assimile à un tirage avec remise).
Enfin, la variable aléatoire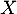 est égale au nombre de succès sur ces 5 répétitions, c'est-à-dire au nombre de coyotes dont le test est positif.
est égale au nombre de succès sur ces 5 répétitions, c'est-à-dire au nombre de coyotes dont le test est positif.
On en déduit que cette variable aléatoire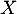 suit la loi binomiale de paramètres
suit la loi binomiale de paramètres
 et
et 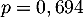 .
.
- La probabilité que dans un échantillon de cinq coyotes capturés au hasard, un seul ait un test positif est, à l'aide de la calculatrice,
![\[P(X=1)\simeq 0,03\]](/Generateur-Devoirs/TS/ChapProbabilites/ex12052022_c/12.png)
- La probabilité qu'au moins quatre coyotes sur cinq aient un test positif est
![\[P(X\geqslant4)\simeq0,52\]](/Generateur-Devoirs/TS/ChapProbabilites/ex12052022_c/13.png)
ce qui montre que l'affirmation du vétérinaire est vraie.
- On répète
- On capture donc
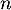 coyotes, et on note
coyotes, et on note 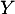 la variable aléatoire égale au
nombre de coyotes ayant un test positif dans cet échantillon.
Comme précédemment,
la variable aléatoire égale au
nombre de coyotes ayant un test positif dans cet échantillon.
Comme précédemment, 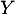 suit la loi binomiale de paramètres
suit la loi binomiale de paramètres 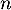 et
et 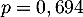 .
.
On cherche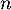 tel que
tel que 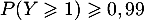
On a
![\[P(Y\geqslant1)=1-P(Y=0)=1-(1-0,694)^n=1-0,306^n\]](/Generateur-Devoirs/TS/ChapProbabilites/ex12052022_c/21.png)
et donc
![\[\begin{array}{ll}&P(Y\geqslant1)\geqslant0,99\\
\iff& 1-0,306^n\geqslant0,99\\
\iff& 0,306^n\leqslant0,01\enar\]](/Generateur-Devoirs/TS/ChapProbabilites/ex12052022_c/22.png)
soit, en prenant le logarithme qui est strictement croissant (donc l'ordre est conservé), puis en divisant par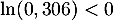 (donc l'ordre est changé):
(donc l'ordre est changé):
![\[\begin{array}{ll}&P(Y\geqslant1)\geqslant0,99\\
\iff&\ln\lp0,306^n\rp=n\ln(0,306)\leqslant\ln(0,01)\\
\iff&n\geqslant\dfrac{\ln(0,01)}{\ln(0,306)}\simeq3,88\enar\]](/Generateur-Devoirs/TS/ChapProbabilites/ex12052022_c/24.png)
Il faut donc capturer au moins 4 coyote.
Cacher la correction
Quelques autres devoirs
Bac blanc: QCM: fonctions, convexité, suite et programme Python - Probabilités: test pour détecter une maladie - Suites: un peu sur les suites - Géométrie dans l'espace - Fonction logarithme
probabilités, loi binomiale et suites de probabilités - suites numériques
Fonction exponentielle - Géométrie dans l'espace - Probabilités, loi binomiale et arbre pondéré - Suite récurrente et python
Bac 2013, Amérique du Sud - Bac 2011, Amérique du nord
sur les probabilités: indépendance d'événements, arbre et probabilités conditionnelles, et le logarithme népérien (ln)
Quelques exercices corrigés
Exercices corrigés
Probabilité de l'intersection
Exercices corrigés
Indépendance de deux événements
Exercices corrigés
Probabilité de vente d'un produit, semaine après semaine
Exercices corrigés
Publicité incitative
Exercices corrigés
Bac 2008 (Nouvelle Calédonie) - Arbre, arbre à inverser, loi binomiale
Voir aussi: