Bac 2008 (Nouvelle Calédonie) - Arbre, arbre à inverser, loi binomiale

Exercice corrigé - Spécialité maths, terminale générale

Deux éleveurs produisent une race de poissons d'ornement qui ne prennent leur couleur définitive qu'à l'âge de trois mois :
  • pour les alevins du premier élevage, entre l'âge de deux mois et l'âge de trois mois, 10 % n'ont pas survécu, 75 % deviennent rouges et les 15 % restant deviennent gris.
  • pour les alevins du deuxième élevage, entre l'âge de deux mois et l'âge de trois mois, 5 % n'ont pas survécu, 65 % deviennent rouges et les 30 % restant deviennent gris.

 
Une animalerie achète les alevins, à l'âge de deux mois : 60 % au premier éleveur, 40 % au second.


  1. Un enfant achète un poisson le lendemain de son arrivée à l'animalerie, c'est-à-dire à l'âge de deux mois.
    1. Montrer que la probabilité que le poisson soit toujours vivant un mois plus tard est de $0,92.
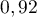    2. Déterminer la probabilité qu'un mois plus tard le poisson soit rouge.
    3. Sachant que le poisson est gris à l'âge de trois mois, quelle est la probabilité qu'il provienne du premier élevage ?

     
  2. Une personne choisit au hasard et de façon indépendante 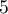$5 alevins de deux mois. Quelle est la probabilité qu'un mois plus tard, seulement trois soient en vie ? On donnera une valeur approchée à 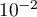$10^{-2} près.
     
  3. L'animalerie décide de garder les alevins jusqu'à l'âge de trois mois, afin qu'ils soient vendus avec leur couleur définitive. Elle gagne 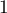$1 euro si le poisson est rouge, 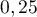$0,25 euro s'il est gris et perd 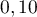$0,10 euro s'il ne survit pas.
     
    Soit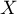 $X la variable aléatoire égale au gain algébrique de l'animalerie par poisson acheté. Déterminer la loi de probabilité de 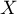$X et son espérance mathématique, arrondie au centime.


Correction


Tag:Probabilités

Autres sujets au hasard: Lancer de dés

Voir aussi:

Quelques devoirs


LongPage: h2: 1 - h3: 0