Géométrie dans l'espace: annales de bac et corrections
Terminale générale, spécialité mathématiques
Annales de bac: sujets et corrigés d'exercices posés au baccalauréat en mathématiques de géométrie dans l'espace
Exercice 1: Bac, 20 mars 2023 - Volume d'un tétraèdre dans un cube
|
On considère le cube ABCDEFCH d'arête 1.
On appelle I le point d'intersection du plan (GBD) avec la droite (EC). L'espace est rapporté au repère orthonormé |
(2.3,1.3)(6.3,1.3)%ADC
\psline[linestyle=dashed](2.3,1.3)(2.3,5.3)%DH
\psline[linestyle=dotted,linewidth=1.2pt](4.8,0.3)(2.3,1.3)(6.3,5.3)%BDG
\psline[linestyle=dotted,linewidth=1.2pt](0.8,4.3)(6.3,1.3)%EC
\uput[d](0.8,0.3){A} \uput[d](4.8,0.3){B} \uput[dr](6.3,1.3){C} \uput[d](2.3,1.3){D}
\uput[u](0.8,4.3){E} \uput[u](4.8,4.3){F} \uput[u](6.3,5.3){G} \uput[u](2.3,5.3){H}
\uput[dl](4.5,2.27){I} \uput[dl](3.55,0.8){J}
\psdots(4.5,2.27)(3.55,0.8)
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapGeomSpace/exBac200323/2.png) |
- Donner dans ce repère les coordonnées des points E, C, G.
- Déterminer une représentation paramétrique de la droite (EC).
- Démontrer que la droite (EC) est orthogonale au plan (GBD).
-
- Justifier qu'une équation cartésienne du plan (GBD) est :
![\[x + y - z - 1 = 0.\]](/Generateur-Devoirs/TS/ChapGeomSpace/exBac200323/3.png)
- Montrer que le point I a pour coordonnées
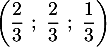 .
.
- En déduire que la distance du point E au plan (GBD) est égale à
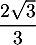 .
.
- Justifier qu'une équation cartésienne du plan (GBD) est :
-
- Démontrer que le triangle BDG est équilatéral.
- Calculer l'aire du triangle BDG. On pourra utiliser le point J, milieu du segment [BD].
- Justifier que le volume du tétraèdre EGBD est égal à
 .
.
On rappelle que le volume d'un tétraèdre est donné par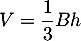 où
où 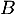 est
l'aire d'une base du tétraèdre et
est
l'aire d'une base du tétraèdre et 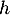 est la hauteur relative à cette base.
est la hauteur relative à cette base.
Correction exercice 1
(Bac spécialité maths, 20 mars 2023)
-
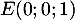 ,
, 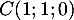 et
et 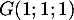 .
.
- On a
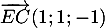 qui dirige
qui dirige  et qui passe par
et qui passe par 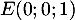 d'où une représentation paramétrique
d'où une représentation paramétrique
![\[(EC):\la\begin{array}{lclcl}
x&=&0&+&t\\
y&=&0&+&t\\
z&=&1&-&t
\enar\right.\ , \ pour t\in\R\]](/Generateur-Devoirs/TS/ChapGeomSpace/exBac200323_c/7.png)
soit
![\[(EC):\la\begin{array}{lcl}
x&=&t\\
y&=&t\\
z&=&1-t
\enar\right.\ , \ pour t\in\R\]](/Generateur-Devoirs/TS/ChapGeomSpace/exBac200323_c/8.png)
- On a
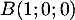 donc
donc 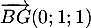 et alors
et alors
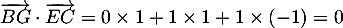
et donc
donc  et alors
et alors
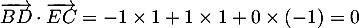
Ainsi,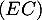 est orthogonale à deux vecteurs non colinéaires du plan
est orthogonale à deux vecteurs non colinéaires du plan 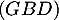 , et donc
, et donc 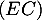 est orthogonale au plan
est orthogonale au plan 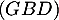 .
.
-
-
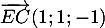 est donc un vecteur normal au plan
est donc un vecteur normal au plan 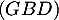 qui a donc une équation cartésienne de la forme
qui a donc une équation cartésienne de la forme
![\[x + y - z + d = 0\]](/Generateur-Devoirs/TS/ChapGeomSpace/exBac200323_c/21.png)
Comme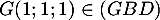 , on a aussi
, on a aussi
![\[1 + 1 - 1 + d = 0\iff d=-1\]](/Generateur-Devoirs/TS/ChapGeomSpace/exBac200323_c/23.png)
d'où l'équation cartésienne
![\[x + y - z - 1 = 0\]](/Generateur-Devoirs/TS/ChapGeomSpace/exBac200323_c/24.png)
- Soit
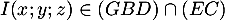 , alors
en utilisant les équations de la représentation paramétrique ainsi que l'équation cartésienne précédente, on obtient
, alors
en utilisant les équations de la représentation paramétrique ainsi que l'équation cartésienne précédente, on obtient
![\[t+t-(1-t)-1=0\iff t=\dfrac23\]](/Generateur-Devoirs/TS/ChapGeomSpace/exBac200323_c/26.png)
Finalement, avec la représentation paramétrique de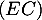 on obtient les coordonnées
on obtient les coordonnées
![\[I\la\begin{array}{lcl}
x&=&t=\frac23\\
y&=&t=\frac23\\
z&=&1-t=\frac13
\enar\right.\]](/Generateur-Devoirs/TS/ChapGeomSpace/exBac200323_c/28.png)
c'est-à-dire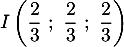 .
.
- La distance du point
 au plan
au plan 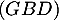 est égale à
est égale à  car
car 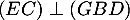 et donc
et donc 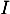 est le projeté orthogonal de
est le projeté orthogonal de 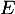 sur
sur 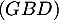 .
.
Cette distance est alors
![\[\begin{array}{ll}EI&=\sqrt{\lp\dfrac23-0\rp^2+\lp\dfrac23-0\rp^2+\lp\dfrac13-1\rp^2}\\
&=\sqrt{3\tm\lp\dfrac23\rp^2}=\dfrac23\sqrt3\enar\]](/Generateur-Devoirs/TS/ChapGeomSpace/exBac200323_c/37.png)
-
-
- On a pour les trois côtés
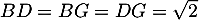 car ce sont les diagonales des faces du cube, donc des diagonales de carrés de côté 1.
car ce sont les diagonales des faces du cube, donc des diagonales de carrés de côté 1.
Ce triangle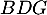 est donc bien équilatéral.
est donc bien équilatéral.
- On a
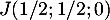 qui est le pied de la médiane issue de
qui est le pied de la médiane issue de  dans le triangle
dans le triangle  . Mais comme ce triangle est équilatéral, cette médiane est aussi la médiatrice et la hauteur, et en particulier le triangle
. Mais comme ce triangle est équilatéral, cette médiane est aussi la médiatrice et la hauteur, et en particulier le triangle  est rectangle en
est rectangle en  et
et
![\[\mathcal{A}_{BDG}=2\tm\mathcal{A}_{BGJ}\]](/Generateur-Devoirs/TS/ChapGeomSpace/exBac200323_c/45.png)
avec
![\[\mathcal{A}_{BGJ}=\dfrac{BJ\times JG}2\]](/Generateur-Devoirs/TS/ChapGeomSpace/exBac200323_c/46.png)
et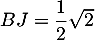 et
et
![\[JG=\sqrt{\lp1-\dfrac12\rp^2+\lp1-\dfrac12\rp^2+(1-0)^2}
=\sqrt{\dfrac32}\]](/Generateur-Devoirs/TS/ChapGeomSpace/exBac200323_c/48.png)
Ainsi, finalement,
![\[\mathcal{A}_{BDG}=\dfrac12\sqrt2\tm\sqrt{\dfrac32}=\dfrac{\sqrt3}2\]](/Generateur-Devoirs/TS/ChapGeomSpace/exBac200323_c/49.png)
- On a pour les trois côtés
- En utilisant comme base
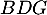 et comme hauteur
et comme hauteur  (qui sont bien orthogonaux d'après les questions précédentes), on trouve
(qui sont bien orthogonaux d'après les questions précédentes), on trouve
![\[\begin{array}{ll}\mathcal{V}_{EGBD}&=\dfrac13\tm\mathcal{A}_{BDG}\tm EI\\[1em]
&=\dfrac13\tm\dfrac{\sqrt3}2\tm\dfrac23\sqrt3\\[1em]
&=\dfrac13\enar\]](/Generateur-Devoirs/TS/ChapGeomSpace/exBac200323_c/52.png)
Cacher la correction
Exercice 2: Bac 2022 - Volume d'un tétraèdre dans un cube
On considère un cube ABCDEFGH
et on appelle K le milieu du segment [BC].
On se place dans le repère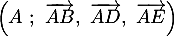 et on considère le tétraèdre EFGK.
et on considère le tétraèdre EFGK.
On rappelle que le volume d'un tétraèdre est donné par:
![\[V=\dfrac13\tm\mathcal{B}\tm h\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022/2.png)
où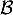 désigne l'aire d'une base et
désigne l'aire d'une base et 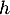 la hauteur relative à cette base.
la hauteur relative à cette base.
(1.5,1.9)(5,1.9)%ADC
\psline[linestyle=dashed](1.5,1.9)(1.5,5.4)%DH
\pspolygon[linestyle=dotted,linewidth=1.25pt](0.2,3.7)(5,5.4)(4.35,1.05)%EGK
\uput[dl](0.2,0.2){\small A}\uput[dr](3.7,0.2){\small B}\uput[r](5,1.9){\small C}
\uput[dr](1.5,1.9){\small D}\uput[l](0.2,3.7){\small E}\uput[r](3.7,3.7){\small F}
\uput[ur](5,5.4){\small G}\uput[ul](1.5,5.4){\small H}\uput[dr](4.35,1.05){\small K}
$$](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022/5.png)
Cacher la correction
On se place dans le repère
On rappelle que le volume d'un tétraèdre est donné par:
où
(1.5,1.9)(5,1.9)%ADC
\psline[linestyle=dashed](1.5,1.9)(1.5,5.4)%DH
\pspolygon[linestyle=dotted,linewidth=1.25pt](0.2,3.7)(5,5.4)(4.35,1.05)%EGK
\uput[dl](0.2,0.2){\small A}\uput[dr](3.7,0.2){\small B}\uput[r](5,1.9){\small C}
\uput[dr](1.5,1.9){\small D}\uput[l](0.2,3.7){\small E}\uput[r](3.7,3.7){\small F}
\uput[ur](5,5.4){\small G}\uput[ul](1.5,5.4){\small H}\uput[dr](4.35,1.05){\small K}
$$](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022/5.png)
- Préciser les coordonnées des points E, F, G et K.
- Montrer que le vecteur
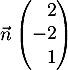 est orthogonal au plan (EGK).
est orthogonal au plan (EGK).
- Démontrer que le plan (EGK) admet pour équation cartésienne :
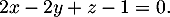
- Déterminer une représentation paramétrique de la droite
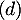 orthogonale au plan (ECK)
passant par F.
orthogonale au plan (ECK)
passant par F.
- Montrer que le projeté orthogonal L de F sur le plan (EGK) a pour coordonnées
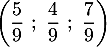 .
.
- Justifier que la longueur LF est égale à
 .
.
- Calculer l'aire du triangle EFG. En déduire que le volume du tétraèdre EFGK est égal à
 .
.
- Déduire des questions précédentes l'aire du triangle EGK.
- On considère les points P milieu du segment [EG], M milieu du segment [EK] et N milieu du segment[GK]. Déterminer le volume du tétraèdre FPMN.
Correction exercice 2
- E( 0 ; 0; 1) ; F( 1 ; 0; 1) ;
G( 1 ; 1 ; 1) ; K( 1 ; 0,5 ; 0)
- On a
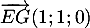 et
et 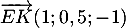 qui sont non colinéaires, et tels que
qui sont non colinéaires, et tels que
![\[\vec{n}\cdot\overrightarrow{EG}=2\tm1+(-2)\tm1+1\tm0=0\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022_c/3.png)
et
![\[\vec{n}\cdot\overrightarrow{EK}=2\tm1+(-2)\tm0,5+1\tm(-1)=0\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022_c/4.png)
et donc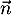 est orthogonal à deux vecteurs colinéaires du plan
(EGK) et donc
est orthogonal à deux vecteurs colinéaires du plan
(EGK) et donc 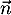 est orthogonal au plan (EGK).
est orthogonal au plan (EGK).
- On déduit de la question précédente qu'une équation cartésienne du plan (EGK)
s'écrit sous la forme
![\[2x-2y+z+d=0\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022_c/7.png)
De plus,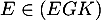 ,
d'où
,
d'où 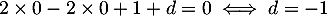 ,
et donc le plan (EGK)
admet bien pour équation cartésienne :
,
et donc le plan (EGK)
admet bien pour équation cartésienne : 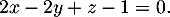
- La droite
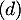 orthogonale au plan (ECK) admet donc
orthogonale au plan (ECK) admet donc 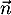 pour vecteur directeur et comme elle passe de plus par F, on peut écrire la représentation paramétrique
pour vecteur directeur et comme elle passe de plus par F, on peut écrire la représentation paramétrique
![\[\la\begin{array}{lclcl}x&=&1&+&2t\\y&=&&-&2t\\z&=&1&+&t\enar\right. \ , \ t\in\R\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022_c/13.png)
- Comme
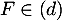 et
et  , le projeté orthogonal L de F
sur le plan (EGK) est l'intersection de la droite et du plan.
, le projeté orthogonal L de F
sur le plan (EGK) est l'intersection de la droite et du plan.
En particulier les coordonnées de L vérifient la représentation paramétrique précédente, pour un certain paramètre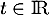 , et aussi l'équation du plan (EGK),
soit
, et aussi l'équation du plan (EGK),
soit
![\[\begin{array}{ll}&2x-2y+z-1=0\\
\iff&2(1+2t)-2(-2t)+(1+t)-1=0\\
\iff&t=-\dfrac29
\enar\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022_c/17.png)
d'où les coordonnées de L:
![\[\la\begin{array}{lclclcl}x&=&1&+&2\lp-\dfrac29\rp&=&\dfrac59\\
y&=&&-&2\lp-\dfrac29\rp&=&\dfrac49\\
z&=&1&+&\lp-\dfrac29\rp&=&\dfrac79\enar\right.\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022_c/18.png)
qui sont bien les coordonnées recherchées. -
![\[\begin{array}{ll}LF&=\sqrt{\lp\dfrac59-1\rp^2+\lp\dfrac49-0\rp^2+\lp\dfrac79-1\rp^2}\\[1.4em]
&=\sqrt{\dfrac{4^2+4^2+2^2}{9^2}}
=\sqrt{\dfrac{36}{9^2}}=\sqrt{\dfrac{4}{9}}=\dfrac23
\enar\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022_c/19.png)
- Le triangle EFG est isocèle rectangle et a pour aire
![\[\mathcal{A}_{EFG}=\dfrac12EF\times EG=\dfrac12\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022_c/20.png)
Dans le tétraèdre EFGK, la hauteur associée à la base EFG est KK',
(1.5,1.9)(5,1.9)%ADC
\psline[linestyle=dashed](1.5,1.9)(1.5,5.4)%DH
\pspolygon[linestyle=dotted,linewidth=1.25pt](0.2,3.7)(5,5.4)(4.35,1.05)%EGK
\uput[dl](0.2,0.2){\small A}\uput[dr](3.7,0.2){\small B}\uput[r](5,1.9){\small C}
\uput[dr](1.5,1.9){\small D}\uput[l](0.2,3.7){\small E}\uput[r](3.7,3.7){\small F}
\uput[ur](5,5.4){\small G}\uput[ul](1.5,5.4){\small H}\uput[dr](4.35,1.05){\small K}
\psline[linecolor=red,linewidth=1.8pt](4.35,1.05)(4.35,4.55)
\rput(4.2,4.7){K'}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022_c/21.png)
On a KK'=1 et donc le volume
![\[\begin{array}{ll}\mathcal{V}_{EFGK}&=\dfrac13\tm\mathcal{A}_{AEFG}\tm KK'\\[1em]
&=\dfrac13\tm\dfrac12\tm1=\dfrac16\enar\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022_c/22.png)
- On eput aussi calculer ce volume en prenant la base EGK,
la hauteur associée étant alors LF, et on a donc
![\[\begin{array}{ll}&\mathcal{V}_{EFGK}=\dfrac13\tm\mathcal{A}_{EGK}\tm LF\\
\iff& \dfrac16=\dfrac13\tm\mathcal{A}_{EGK}\tm\dfrac23\\
\iff&\mathcal{A}_{EGK}=\dfrac34
\enar\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022_c/23.png)
-
(1.5,1.9)(5,1.9)%ADC
\psline[linestyle=dashed](1.5,1.9)(1.5,5.4)%DH
\pspolygon[linestyle=dotted,linewidth=1.25pt](0.2,3.7)(5,5.4)(4.35,1.05)%EGK
\uput[dl](0.2,0.2){\small A}\uput[dr](3.7,0.2){\small B}\uput[r](5,1.9){\small C}
\uput[dr](1.5,1.9){\small D}\uput[l](0.2,3.7){\small E}\uput[r](3.7,3.7){\small F}
\uput[ur](5,5.4){\small G}\uput[ul](1.5,5.4){\small H}\uput[dr](4.35,1.05){\small K}
%
\pspolygon[linecolor=blue](2.6,4.55)(2.275,2.375)(4.675,3.225)%PMN
\psline[linecolor=blue](2.6,4.55)(3.7,3.7)
\psline[linecolor=blue](2.275,2.375)(3.7,3.7)
\psline[linecolor=blue](4.675,3.225)(3.7,3.7)
\rput(2.4,4.7){\blue P}
\rput(2,2.2){\blue M}
\rput(4.84,3.){\blue N}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022_c/24.png)
Comme les deux triangles EGK et PMN sont dans le même plan, les hauteurs qui leurs sont associées dans les deux trétraèdres sont les mêmes, soit LF.
D'arpès le théorème de Thalès, on a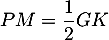 ,
,
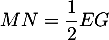 et
et 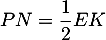 : les longueurs de tous les côtés sont divisées par 2, et l'aire est donc divisée par 4.
: les longueurs de tous les côtés sont divisées par 2, et l'aire est donc divisée par 4.
Finalement, on obtient l'aire du tétraèdre:
![\[\begin{array}{ll}
\mathcal{V}_{FPMN}&=\dfrac13\tm\mathcal{A}_{PMN}\tm LF\\
&=\dfrac13\tm\lp\dfrac14\tm\dfrac34\rp\tm\dfrac23\\
&=\dfrac1{24}
\enar\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex12052022_c/28.png)
Cacher la correction
Exercice 3: Représentation paramétrique et projeté orthogonal
Dans l'espace rapporté à un repère orthonormé 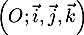 ,
on considère:
,
on considère:
Cacher la correction
- le point A de coordonnées
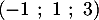 ,
, - la droite
 dont une représentation paramétrique est:
dont une représentation paramétrique est:
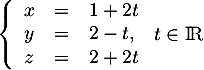 .
.
-
- Donner les coordonnées d'un vecteur directeur
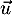 de la droite
de la droite  .
On admet que le point A n'appartient pas à la droite
.
On admet que le point A n'appartient pas à la droite  .
.
- Montrer que le point
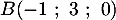 appartient à la droite
appartient à la droite  .
.
- Calculer le produit scalaire
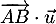 .
.
- Donner les coordonnées d'un vecteur directeur
- On note
 le plan passant par le point A et orthogonal à la droite
le plan passant par le point A et orthogonal à la droite 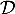 , et on appelle H le point d'intersection du plan
, et on appelle H le point d'intersection du plan 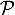 et de la droite
et de la droite  . Ainsi, H est le projeté orthogonal de A sur la droite
. Ainsi, H est le projeté orthogonal de A sur la droite  .
.
- Montrer que le plan
 admet pour équation cartésienne:
admet pour équation cartésienne: 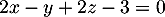 .
.
- En déduire que le point H a pour coordonnées
 .
.
- Calculer la longueur AH. On donnera une valeur exacte.
- Montrer que le plan
- Dans cette question, on se propose de retrouver les coordonnées du point H, projeté orthogonal du point A sur la droite
 , par une autre méthode.
On rappelle que le point B
, par une autre méthode.
On rappelle que le point B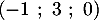 appartient à la droite
appartient à la droite  et que le vecteur
et que le vecteur  est un vecteur directeur de la droite
est un vecteur directeur de la droite 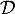 .
.
- Justifier qu'il existe un nombre réel
 tel que
tel que 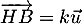 .
.
- Montrer que
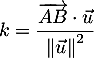 .
.
- Calculer la valeur du nombre réel
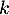 et retrouver les coordonnées du point H.
et retrouver les coordonnées du point H.
- Justifier qu'il existe un nombre réel
- On considère un point C appartenant au plan
 tel que le volume du tétraèdre ABCH soit égal à
tel que le volume du tétraèdre ABCH soit égal à  .
Calculer l'aire du triangle ACH.
.
Calculer l'aire du triangle ACH.
On rappelle que le volume d'un tétraèdre est donné par: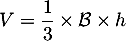 où
où  désigne l'aire d'une base
et
désigne l'aire d'une base
et 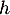 la hauteur relative à cette base.
la hauteur relative à cette base.
Correction exercice 3
-
- Un vecteur directeur est donné par
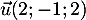
- Avec les coordonnées de B, on a
![\[\la\begin{array}{lcl}
-1&=&1+2t\\3 &=& 2 - t,\\0&=& 2+2t
\enar\right.
\iff
\la\begin{array}{lcl}
t&=&-1\\t&=&-1,\\t&=&-1
\enar\right.\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/2.png)
ce qui montre que B appartient bien à la droite .
.
- On a
 donc
donc
![\[\overrightarrow{AB}\cdot\vec{u}=0\tm2+2\tm(-1)+(-3)\tm2=-8\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/5.png)
- Un vecteur directeur est donné par
-
(4,0)
\psline(4,0)(4,-2)
\rput(4,1){$\tm$}\rput(4.3,1.2){$H$}
\rput(3.7,3.5){$\mathcal{D}$}
\psline[linecolor=blue,linewidth=2pt]{->}(4,-1.5)(4,-.5)
\psline[linecolor=blue](3.92,-1.5)(4.08,-1.5)
\rput(4.25,-1.1){\blue$\vec{u}$}
\rput(4,2.6){$\tm$}\rput(4.3,2.7){$B$}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/6.png)
- Le plan
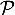 est orthogonale à la droite
est orthogonale à la droite 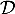 dirigée par
dirigée par
 qui est donc un vecteur normal à ce plan qui admet
donc une équation cartésienne de la forme
qui est donc un vecteur normal à ce plan qui admet
donc une équation cartésienne de la forme
![\[2x-y+2z+d=0\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/10.png)
On sait de plus que , et donc que
, et donc que
![\[2(-1)-(1)+2(3)+d=0\iff d=-3\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/12.png)
Finalement, on a trouvé une équation cartésienne du plan :
:
![\[\mathcal{P}: 2x - y + 2z - 3 = 0\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/14.png)
- Le plan
 et la droite
et la droite  sont orthogonaux;
en particulier ils se coupent en un unique point
sont orthogonaux;
en particulier ils se coupent en un unique point 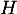 .
.
Soit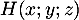 , alors
, alors
![\[H\in\mathcal{D}\iff
\la\begin{array}{lcl}
x&=&1+2t\\y &=& 2 - t,\\z&=& 2+2t
\enar\right. t \in \R\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/19.png)
et de plus,
![\[\begin{array}{ll}H\in\mathcal{P}&\iff 2x - y + 2z - 3 = 0\\
&\iff2(1+2t)-(2-t)+2(2+2t)-3=0\\
&\iff t=-\dfrac19
\enar\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/20.png)
et on obtient alors les coordonnées
![\[\la\begin{array}{lcl}
x&=&1+2\tm\lp-1\frac19\rp=\frac79\\[.4em]
y &=& 2 - \lp-\frac19\rp=\frac{19}9\\[.4em]
z&=& 2+2\lp-\frac19\rp=\frac{16}9
\enar\right. t \in \R\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/21.png)
qui sont bien les coordonnées recherchées du point H.
-
![\[\begin{array}{ll}
AH&=\sqrt{\lp\dfrac79-(-1)\rp^2+\lp\dfrac{19}9-1\rp^2+\lp\dfrac{16}9-3\rp^2}\\
&=\sqrt{\dfrac{16^2+10^2+11^2}{9^2}}
=\dfrac{\sqrt{253}}9
\enar\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/22.png)
- Le plan
-
- Les points H et B appartiennent tous les deux à la droite
 ,
et
,
et  est un vecteur directeur de cette droite.
est un vecteur directeur de cette droite.
On en déduit que les vecteurs et
et 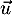 sont colinéaires,
c'est-à-dire qu'il existe un réel
sont colinéaires,
c'est-à-dire qu'il existe un réel 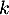 tel que
tel que
 .
.
- D'après le résultat précédent, en prenant le produit scalaire
avec
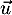 on obtient
on obtient
![\[\overrightarrow{HB}=k\vec{u}\implies \overrightarrow{HB}\cdot\vec{u}=k\vec{u}\cdot\vec{u}=\left\|\vec{u}\right\|^2\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/30.png)
d'où
![\[k=\dfrac{\overrightarrow{HB}\cdot\vec{u}}{\left\|\vec{u}\right\|^2}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/31.png)
Maintenant pour faire intervenir le vecteur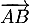 on peut utiliser la
relation de Chasles:
on peut utiliser la
relation de Chasles:
![\[\overrightarrow{HB}=\overrightarrow{HA}+\overrightarrow{AB}
\implies
\overrightarrow{HB}\cdot\vec{n}=\overrightarrow{HA}\cdot\vec{n}+\overrightarrow{AB}\cdot\vec{n}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/33.png)
or car
car 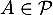 et
et  et
et  normal à
normal à  .
.
On vient donc de trouver que
![\[\overrightarrow{HB}\cdot\vec{n}=\overrightarrow{AB}\cdot\vec{n}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/39.png)
et donc la relation souhaitée:
![\[k=\dfrac{\overrightarrow{HB}\cdot\vec{u}}{\left\|\vec{u}\right\|^2}
=\dfrac{\overrightarrow{AB}\cdot\vec{u}}{\left\|\vec{u}\right\|^2}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/40.png)
-
D'après la question 1.c. on a
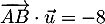 ,
et comme
,
et comme 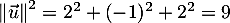 , on obtient
que
, on obtient
que
![\[k=\dfrac{-8}9\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/43.png)
et on retrouve les coordonnées du point H(x;y;z):
![\[\overrightarrow{HB}=k\vec{u}
\iff
\la\begin{array}{lcl}
-1-x&=&-\dfrac89\tm2\\
3-y&=&-\dfrac89\tm(-1)\\
0-z&=&-\dfrac89\tm2
\enar\right.
\iff
\la\begin{array}{lcl}
x&=&-1+\dfrac{16}9=\dfrac79\\
y&=&3-\dfrac89=\dfrac{19}9\\
z&=&\dfrac{16}9
\enar\right.
\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/44.png)
- Les points H et B appartiennent tous les deux à la droite
- BH est une hauteur relative à la base ACH,
et donc, avec
![\[V = \dfrac13 \times \mathcal{B} \times h\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/45.png)
avec
![\[\begin{array}{ll}
h&=BH=\sqrt{\lp\dfrac79-(-1)\rp^2+\lp\dfrac{19}9-3\rp^2+\lp\dfrac{16}9-0\rp^2}\\
&=\sqrt{\dfrac{16^2+8^2+16^2}{9^2}}
=\dfrac{8}{9}\sqrt{9}=\dfrac{24}9
\enar\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/46.png)
et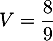 ,
d'où l'aire de la base ACH:
,
d'où l'aire de la base ACH:
![\[\dfrac89=\dfrac13\tm\mathcal{B}\tm\dfrac{24}{9}
\iff
\mathcal{B}=1\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex11052022_c/48.png)
Cacher la correction
Exercice 4: Bac 2021 - Géométrie dans un cube
|
On considère le cube Dans tous les exercices, l'espace est rapporté au repère orthonormé |

\psline(4,0.5)(4,3.5)
\psline(4,3.5)(1,3.5)
\psline(0,3)(1,3.5)
\psline(3,3)(4,3.5)
\psline[linestyle=dashed](1,0.5)(4,0.5)
\psline[linestyle=dashed](3,0)(4,.5)
\psline[linestyle=dashed](1,0.5)(1,3.5)
\rput(-0.2,-0.2){$A$}
\rput(3.2,-0.2){$B$}
\rput(4.3,0.6){$C$}
\rput(1.2,0.7){$D$}
\rput(-.2,3){$E$}
\rput(2.95,3.2){$F$}
\rput(4.3,3.7){$G$}
\rput(.7,3.7){$H$}
\rput(1.5,2.98){$\tm$}\rput(1.5,2.65){$I$}
\psline[linewidth=.5pt](3,3)(6,3)
\rput(6,2.98){$\tm$}\rput(5.9,2.65){$J$}
$$](/Generateur-Devoirs/TS/ChapGeomSpace/ex0/8.png) |
-
- Par lecture graphique, donner les coordonnées de
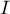 et
et 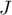 .
.
- En déduire les coordonnées des vecteurs
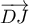 ,
, 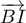 et
et  .
.
- Montrer que
 est un vecteur normal au plan
est un vecteur normal au plan  .
.
- Montrer qu'une équation cartésienne du plan
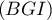 est
est
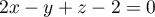 .
.
- Par lecture graphique, donner les coordonnées de
- On note
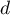 la droite passant par
la droite passant par 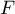 et orthogonale au plan
et orthogonale au plan  .
.
- Déterminer une représentation paramétrique de la droite
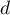 .
.
- On considère le point
 de coordonnées
de coordonnées
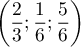 .
.
Montrer que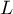 est le point d'intersection de la droite
est le point d'intersection de la droite 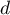 et du plan
et du plan 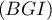 .
.
- Déterminer une représentation paramétrique de la droite
- On rappelle que le volume
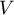 d'une pyramide est donné par la formule
d'une pyramide est donné par la formule
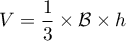 ,
où
,
où  est l'aire d'une base et
est l'aire d'une base et 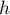 la hauteur associée à cette base.
la hauteur associée à cette base.
- Calculer le volume de la pyramide
 .
.
- En déduire l'aire du triangle
 .
.
- Calculer le volume de la pyramide
Correction exercice 4

\psline(4,0.5)(4,3.5)
\psline(4,3.5)(1,3.5)
\psline(0,3)(1,3.5)
\psline(3,3)(4,3.5)
\psline[linestyle=dashed](1,0.5)(4,0.5)
\psline[linestyle=dashed](3,0)(4,.5)
\psline[linestyle=dashed](1,0.5)(1,3.5)
\rput(-0.2,-0.2){$A$}
\rput(3.2,-0.2){$B$}
\rput(4.3,0.6){$C$}
\rput(1.2,0.7){$D$}
\rput(-.2,3){$E$}
\rput(2.95,3.2){$F$}
\rput(4.3,3.7){$G$}
\rput(.7,3.7){$H$}
\rput(1.5,2.98){$\tm$}\rput(1.5,2.65){$I$}
\psline[linewidth=.5pt](3,3)(6,3)
\rput(6,2.98){$\tm$}\rput(5.9,2.65){$J$}
$$](/Generateur-Devoirs/TS/ChapGeomSpace/ex0_c/1.png) |
-
- Par lecture graphique,
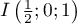 et
et 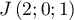 .
.
- On en déduit
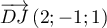 ,
,
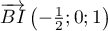 et
et
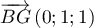 .
.
-
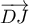 est normal au plan
est normal au plan 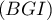 si et seulement si il est orthogonal à deux vecteurs non colinéaires du plan, par exemple
si et seulement si il est orthogonal à deux vecteurs non colinéaires du plan, par exemple
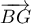 et
et 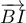 , ce qui est bien le cas car:
, ce qui est bien le cas car:
![\[\overrightarrow{DJ}\cdot\overrightarrow{BG}=2\tm0+(-1)\tm1+1\tm1=0\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex0_c/11.png)
et
![\[\overrightarrow{DJ}\cdot\overrightarrow{BI}=2\tm\lp-\dfrac12\rp+(-1)\tm0+1\tm1=0\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex0_c/12.png)
- Un vecteur normal au plan
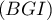 est donc
est donc 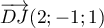 et donc ce plan a une équation cartésienne de la forme
et donc ce plan a une équation cartésienne de la forme
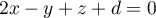 .
.
De plus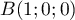 appartient à ce plan, d'où
appartient à ce plan, d'où
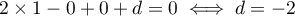 .
.
Une équation cartésienne du plan est donc bien
est donc bien
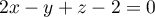 .
.
- Par lecture graphique,
- On note
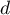 la droite passant par
la droite passant par 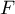 et orthogonale au plan
et orthogonale au plan  .
.
- Comme la droite
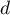 est orthogonale au plan
est orthogonale au plan  et que
et que 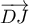 est aussi orthogonal à ce plan, on en déduit que
est aussi orthogonal à ce plan, on en déduit que 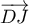 est un vecteur directeur de
est un vecteur directeur de  . On a donc une reprsentation paramétrique, avec
. On a donc une reprsentation paramétrique, avec 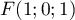 :
:
![\[d:\la\begin{array}{ccr}
x&=&1+2t\\
y&=&-t\\
z&=&1+t\enar\right.
\ , t \in\R\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex0_c/29.png)
- Comme
 est orthogonal à
est orthogonal à  , leur intersection est donc un point. Il reste donc simplement à vérifier que cette intersection est le point
, leur intersection est donc un point. Il reste donc simplement à vérifier que cette intersection est le point  , c'est-à-dire que
, c'est-à-dire que 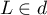 et
et 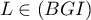 .
.
Avec l'équation cartésienne de ,
,
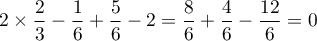 et donc
et donc 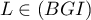 .
.
Avec la représentation prarémtrique de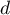 , on cherche
, on cherche 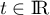 tel que
tel que
![\[d:\la\begin{array}{ccl}
\frac23&=&1+2t\\[.4em]
\frac16&=&-t\\[.4em]
\frac56&=&1+t\enar\right.
\iff t=-\dfrac16\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex0_c/40.png)
et donc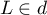 .
.
Finalement est le point d'intersection de
est le point d'intersection de  et
et  .
.
- Comme la droite
-
- D'après tout ce qui précède, une hauteur est
 associée à la base
associée à la base 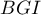 .
.
On peut aussi considérer la base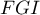 associée à la hauteur
associée à la hauteur 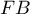 , qui donne
le volume
, qui donne
le volume
![\[\begin{array}{ll}V&=\dfrac13\tm\lp\dfrac12 FI\tm FG\rp\tm FB\\[1em]
&=\dfrac13\tm\lp\dfrac12\tm\dfrac12\tm1\rp\tm1
=\dfrac1{12}
\enar\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex0_c/49.png)
- En utilisant la hauteur
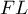 et la base
et la base  d'aire
d'aire  ,
on a
,
on a
![\[V=\dfrac13\tm\mathcal{B}\tm FL\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex0_c/53.png)
où
![\[FL=\sqrt{\lp\dfrac23-1\rp^2+\lp\dfrac16-0\rp^2+\lp\dfrac56-1\rp^2}
=\sqrt{\dfrac16}
=\dfrac1{\sqrt6}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex0_c/54.png)
On en déduit que
![\[V=\dfrac1{12}=\dfrac13\tm\mathcal{B}\tm\dfrac1{\sqrt6}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex0_c/55.png)
d'où l'aire du triangle .
.
![\[\mathcal{B}=\dfrac{\sqrt6}4\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex0_c/57.png)
- D'après tout ce qui précède, une hauteur est
Cacher la correction
Exercice 5: Bac 2021, Amérique du nord - Géométrie dans un cube et représentation paramétrique de droites
On considère un cube ABCDEFGH. Le point I est le milieu du segment [EF], le point J est le milieu du segment [BC] et le point K est le milieu du segment [AE].
{A} \uput[dr](5.5,0){B} \uput[u](5.5,5){F} \uput[ul](0.5,5.4){E}
\psline(5.5,0)(8.5,1.4)(8.5,6.4)(5.5,5)%BCGF
\uput[r](8.5,1.4){C} \uput[ur](8.5,6.4){G}
\psline(8.5,6.4)(3.5,6.8)(0.5,5.4)%GHE
\uput[u](3.5,6.8){H} \uput[u](3,5.2){I}\uput[dr](7,0.7){J}\uput[l](0.5,2.9){K}
\psline[linewidth=1.6pt](0.5,0.4)(3,5.2)%AI
\psline[linestyle=dashed,linewidth=1.6pt](3,5.2)(7,0.7)%IJ
\psline[linestyle=dashed,linewidth=1.6pt](0.5,2.9)(3.5,6.8)%KH
\psline[linestyle=dashed](0.5,0.4)(3.5,1.8)(3.5,6.8)%ADH
\uput[ur](3.5,1.8){D}
\psline[linestyle=dashed](3.5,1.8)(8.5,1.4)%DC
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapGeomSpace/exAN21/1.png)
Baccalauréat général, spécialité mathématique, Amérique du Nord mai 2021 (candidats libres)
{A} \uput[dr](5.5,0){B} \uput[u](5.5,5){F} \uput[ul](0.5,5.4){E}
\psline(5.5,0)(8.5,1.4)(8.5,6.4)(5.5,5)%BCGF
\uput[r](8.5,1.4){C} \uput[ur](8.5,6.4){G}
\psline(8.5,6.4)(3.5,6.8)(0.5,5.4)%GHE
\uput[u](3.5,6.8){H} \uput[u](3,5.2){I}\uput[dr](7,0.7){J}\uput[l](0.5,2.9){K}
\psline[linewidth=1.6pt](0.5,0.4)(3,5.2)%AI
\psline[linestyle=dashed,linewidth=1.6pt](3,5.2)(7,0.7)%IJ
\psline[linestyle=dashed,linewidth=1.6pt](0.5,2.9)(3.5,6.8)%KH
\psline[linestyle=dashed](0.5,0.4)(3.5,1.8)(3.5,6.8)%ADH
\uput[ur](3.5,1.8){D}
\psline[linestyle=dashed](3.5,1.8)(8.5,1.4)%DC
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapGeomSpace/exAN21_c/1.png)
Cacher la correction
{A} \uput[dr](5.5,0){B} \uput[u](5.5,5){F} \uput[ul](0.5,5.4){E}
\psline(5.5,0)(8.5,1.4)(8.5,6.4)(5.5,5)%BCGF
\uput[r](8.5,1.4){C} \uput[ur](8.5,6.4){G}
\psline(8.5,6.4)(3.5,6.8)(0.5,5.4)%GHE
\uput[u](3.5,6.8){H} \uput[u](3,5.2){I}\uput[dr](7,0.7){J}\uput[l](0.5,2.9){K}
\psline[linewidth=1.6pt](0.5,0.4)(3,5.2)%AI
\psline[linestyle=dashed,linewidth=1.6pt](3,5.2)(7,0.7)%IJ
\psline[linestyle=dashed,linewidth=1.6pt](0.5,2.9)(3.5,6.8)%KH
\psline[linestyle=dashed](0.5,0.4)(3.5,1.8)(3.5,6.8)%ADH
\uput[ur](3.5,1.8){D}
\psline[linestyle=dashed](3.5,1.8)(8.5,1.4)%DC
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapGeomSpace/exAN21/1.png)
-
Les droites (AI) et (KH) sont-elles parallèles ? Justifier votre réponse,
Dans la suite, on se place dans le repère orthonormé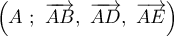 .
.
-
- Donner les coordonnées des points I et J.
- Montrer que les vecteurs
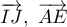 et
et 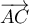 sont coplanaires.
sont coplanaires.
On considère le plan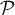 d'équation
d'équation 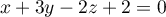 ainsi que les droites
ainsi que les droites 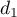 et
et 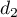 définies par les représentations
paramétriques ci-dessous:
définies par les représentations
paramétriques ci-dessous:
![\[d_1 : \left\{\begin{array}{l c l}
x &=&3 + t\\
y &=& 8 - 2t\\
z &=& - 2 + 3t\\
\end{array}\right. , t \in \R\quad \text{et}\quad
d_2 : \left\{\begin{array}{l c l}
x &=&4 + t\\
y &=&1 + t\\
z &=&8 + 2t\\
\end{array}\right. , t \in \R.\]](/Generateur-Devoirs/TS/ChapGeomSpace/exAN21/9.png)
- Les droites
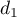 et
et 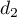 sont-elles parallèles ? Justifier votre réponse.
sont-elles parallèles ? Justifier votre réponse.
- Montrer que la droite
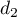 est parallèle au plan
est parallèle au plan  .
.
- Montrer que le point L(4 ; 0 ; 3) est le projeté orthogonal du point M(5 ; 3 ; 1) sur le plan
 .
.
Correction exercice 5
Baccalauréat général, spécialité mathématique, Amérique du Nord mai 2021 (candidats libres)
{A} \uput[dr](5.5,0){B} \uput[u](5.5,5){F} \uput[ul](0.5,5.4){E}
\psline(5.5,0)(8.5,1.4)(8.5,6.4)(5.5,5)%BCGF
\uput[r](8.5,1.4){C} \uput[ur](8.5,6.4){G}
\psline(8.5,6.4)(3.5,6.8)(0.5,5.4)%GHE
\uput[u](3.5,6.8){H} \uput[u](3,5.2){I}\uput[dr](7,0.7){J}\uput[l](0.5,2.9){K}
\psline[linewidth=1.6pt](0.5,0.4)(3,5.2)%AI
\psline[linestyle=dashed,linewidth=1.6pt](3,5.2)(7,0.7)%IJ
\psline[linestyle=dashed,linewidth=1.6pt](0.5,2.9)(3.5,6.8)%KH
\psline[linestyle=dashed](0.5,0.4)(3.5,1.8)(3.5,6.8)%ADH
\uput[ur](3.5,1.8){D}
\psline[linestyle=dashed](3.5,1.8)(8.5,1.4)%DC
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapGeomSpace/exAN21_c/1.png)
- On a A(0;0;0) et I(0,5;0;1), donc
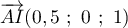 et K(0;0;0,5) et H(0;1;1)
donc
et K(0;0;0,5) et H(0;1;1)
donc 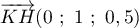 .
.
Ces vecteurs ne sont pas colinéaires, donc les droites (AI) et (KH) ne sont pas parallèles.
-
- On a par lecture graphique I(0,5;0;1), et J(1;0,5;0)
- On a
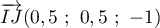 ,
, 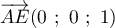 , et
, et
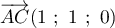 .
.
On a donc que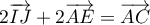 ,
ce qui montre que ces trois vecteurs sont coplanaires.
,
ce qui montre que ces trois vecteurs sont coplanaires.
Autre méthode 2, si on ne s'aperçoit pas de la relation suivante, on peut tous simplement la chercher: on cherche s'il existe trois réels a,b et c tels que
![\[a\overrightarrow{IJ}+b\overrightarrow{AE}+c\overrightarrow{AC}=\vec{0}
\iff\la\begin{array}{rcrcrcl}
0,5a&+& &+&c &=&0\\
0,5a&+& &+&c &=&0\\
-a&+& b&& &=&0\enar\right.\]](/Generateur-Devoirs/TS/ChapGeomSpace/exAN21_c/8.png)
dont la troisième équation donne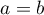 puis
puis  , et il y a une infinité de solutions, par
exemple
, et il y a une infinité de solutions, par
exemple  et
et  ,
d'où la relation
,
d'où la relation
![\[\overrightarrow{IJ}+\overrightarrow{AE}-0,5\overrightarrow{AC}=\vec{0}
\iff \overrightarrow{IJ}=-\overrightarrow{AE}+0,5\overrightarrow{AC}\]](/Generateur-Devoirs/TS/ChapGeomSpace/exAN21_c/13.png)
 a pour vecteur directeur
a pour vecteur directeur 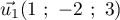 et
et 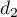 a pour vecteur directeur
a pour vecteur directeur 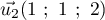 : ces vecteurs ne sont pas colinéaires, donc les droites
: ces vecteurs ne sont pas colinéaires, donc les droites 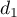 et
et 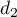 ne sont pas parallèles
ne sont pas parallèles
- Un vecteur directeur de
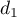 est
est 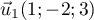 et un vecteur directeur de
et un vecteur directeur de 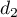 est
est 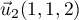 .
.
Ces deux vecteurs ne sont pas colinéaires donc les droites ne sont pas parallèles.
- Le plan a pour vecteur normal le vecteur
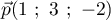 et
et 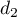 a pour vecteur directeur
a pour vecteur directeur 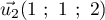 .
.
Or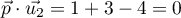 :
les vecteurs sont orthogonaux donc la droite
:
les vecteurs sont orthogonaux donc la droite 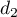 est parallèle
au plan
est parallèle
au plan  .
.
-
Méthode 1. Soit
 la perpendiculaire à
la perpendiculaire à  contenant M. Cette droite a pour vecteur directeur le vecteur
contenant M. Cette droite a pour vecteur directeur le vecteur  , donc une équation paramétrique de
, donc une équation paramétrique de  est :
est :
![\[\la\begin{array}{rcl}
x&=&5 + 1t\\
y&=&3 + 3t\\
z&=&1 - 2t\\
\enar\right., t \in \R.\]](/Generateur-Devoirs/TS/ChapGeomSpace/exAN21_c/34.png)
Le projeté L, de M sur le plan a ses coordonnées qui vérifient les quatre équations:
a ses coordonnées qui vérifient les quatre équations:
![\[\left\{\begin{array}{rcl}
x&=&5 + 1t\\
y&=&3 + 3t\\
z&=&1 - 2t\\
x + 3y - 2z + 2&=&0
\end{array}\right. , t \in \R.\]](/Generateur-Devoirs/TS/ChapGeomSpace/exAN21_c/36.png)
et donc, en substituant les expressions des coordonnées dans la dernière équation du plan, on obtient
![\[5 + t + 3(3 + 3t) - 2(1 - 2t) + 2 = 0
\iff t = - 1\]](/Generateur-Devoirs/TS/ChapGeomSpace/exAN21_c/37.png)
En reportant dans les trois premières équations du système, on trouve alors les coordonnées de L projeté orthogonal de M sur :
:
![\[\la\begin{array}{lcl}
x&=&5 - 1\\
y&=&3 + 3\times (- 1)\\
z&=&1 - 2\times (- 1)\\
\enar\right. \iff
\la\begin{array}{l c l}
x&=&4\\
y&=&0\\
z&=&3\\
\enar\right.\]](/Generateur-Devoirs/TS/ChapGeomSpace/exAN21_c/39.png)
Donc le projeté orthogonal de M sur le plan est le le point L(4 ; 0 ; 3).
est le le point L(4 ; 0 ; 3).
Méthode 2. On a ,
donc
,
donc  est un vecteur normal au plan
est un vecteur normal au plan 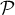 .
.
D'autre part
![\[L(4~;~0~;~3)\in\mathcal{P}\iff 4 + 3 \times 0 - 2 \times 3 + 2 = 6 - 6 = 0\]](/Generateur-Devoirs/TS/ChapGeomSpace/exAN21_c/44.png)
est vraie, donc L est bien le projeté orthogonal de M sur le plan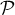 .
.
Cacher la correction
Exercice 6: Bac 2021 - QCM de géométrie dans l'espace
Cet exercice est un questionnaire à choix multiples.
Pour chacune des questions suivantes, une seule des quatre réponses proposées
est exacte.
Une réponse exacte rapporte un point. Une réponse fausse, une réponse multiple ou l'absence de réponse à une question ne rapporte ni n'enlève de point.
Pour répondre, indiquer sur la copie le numéro de la question et la lettre de la réponse choisie.
Aucune justification n'est demandée.
(8,1.8)(3,1.8)(0,0)%BADB
\psline[linestyle=dashed](5,0)(3,1.8)(4,4)(4,0.95)%CASI
\psline(0,0)(4,4)(5,0)(8,1.8)(4,4)%DSCBS
\uput[dl](0,0){D}\uput[dr](5,0){C}\uput[ur](8,1.8){B}\uput[ul](3,1.8){A}
\uput[u](4,4){S}\uput[d](4,0.95){I}
\uput[ul](2,2){K}\uput[ur](4.5,2){L}\uput[ur](6,2.9){M}
\psdots[dotstyle=+,dotangle=30,dotscale=1.85](2,2)(4.5,2)(6,2.9)
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex150321QCM/1.png)
SABCD est une pyramide régulière à base carrée ABCD dont toutes les arêtes ont la même longueur.
Le point I est le centre du carré ABCD. On suppose que: IC = IB = IS = 1.
Les points K, L et M sont les milieux respectifs des arêtes [SD], [SC] et [SB].
Cacher la correction
Une réponse exacte rapporte un point. Une réponse fausse, une réponse multiple ou l'absence de réponse à une question ne rapporte ni n'enlève de point.
Pour répondre, indiquer sur la copie le numéro de la question et la lettre de la réponse choisie.
Aucune justification n'est demandée.
(8,1.8)(3,1.8)(0,0)%BADB
\psline[linestyle=dashed](5,0)(3,1.8)(4,4)(4,0.95)%CASI
\psline(0,0)(4,4)(5,0)(8,1.8)(4,4)%DSCBS
\uput[dl](0,0){D}\uput[dr](5,0){C}\uput[ur](8,1.8){B}\uput[ul](3,1.8){A}
\uput[u](4,4){S}\uput[d](4,0.95){I}
\uput[ul](2,2){K}\uput[ur](4.5,2){L}\uput[ur](6,2.9){M}
\psdots[dotstyle=+,dotangle=30,dotscale=1.85](2,2)(4.5,2)(6,2.9)
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex150321QCM/1.png)
SABCD est une pyramide régulière à base carrée ABCD dont toutes les arêtes ont la même longueur.
Le point I est le centre du carré ABCD. On suppose que: IC = IB = IS = 1.
Les points K, L et M sont les milieux respectifs des arêtes [SD], [SC] et [SB].
- Les droites suivantes ne sont pas coplanaires:
a. (DK) et (SD) b. (AS) et (IC) c. (AC) et (SB) d. (LM) et (AD)
Pour les questions suivantes, on se place dans le repère orthonormé de l'espace .
.
Dans ce repère, on donne les coordonnées des points suivants:
![\[I(0;0;0) \ ; \
A(-1;0;0) \ ; \
B(0;1;0) \ ; \
C(1;0;0) \ ; \
D(0;-1;0) \ ; \
S(0;0;1)\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex150321QCM/3.png)
- Les coordonnées du milieu N de [KL] sont:
a.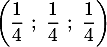 b.
b. 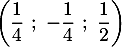 c.
c.  d.
d. 
- Les coordonnées du vecteur
 sont:
sont:
a. b.
b. 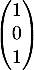 c.
c. 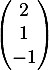 d.
d. 
- Une représentation paramétrique de la droite (AS) est:
a.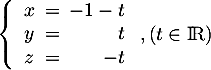 b.
b. 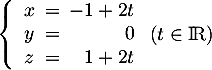 c.
c. 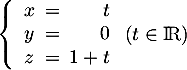 d.
d. 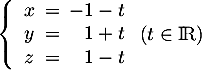
- Une équation cartésienne du plan (SCB) est:
a.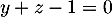 b.
b.  c.
c. 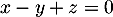 &
d.
&
d. 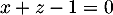
Correction exercice 6
- Réponse c.
On peut procèder par élimination:- Les droites (DK) et (SD) sont sécantes en D donc coplanaires; on élimine a.
- Les droites (AS) et (IC) sont sécantes en A donc coplanaires; on élimine b.
- Les droites (LM) et (AD) sont toutes deux parallèles à (BC) donc parallèles entre elles; elles sont donc coplanaires; on élimine d.
- Réponse b.
On calcule les coordonnées des milieux: le milieu K de [SD] a pour coordonnées ,
et le milieu L de [SC] a pour coordonnées
,
et le milieu L de [SC] a pour coordonnées
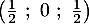 ,
et enfin le milieu N de [KL] a donc pour coordonnées
,
et enfin le milieu N de [KL] a donc pour coordonnées
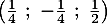 .
.
- Réponse b.
- Réponse c.
La droite (AS) a pour vecteur directeur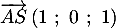 et donc
la seule représentation qui convienne est la c.
et donc
la seule représentation qui convienne est la c.
- Réponse b.
On peut là aussi procèder par élimination:- Le plan d'équation
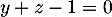 ne contient pas C
ne contient pas C  ; on élimine a.
; on élimine a.
- Le plan d'équation
 ne contient pas S
ne contient pas S 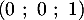 ; on élimine c.
; on élimine c.
- Le plan d'équation
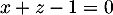 ne contient pas B
ne contient pas B  ; on élimine d.
; on élimine d.
- Le plan d'équation
Cacher la correction
Exercice 7: Bac 2021 - Distance point à un plan et volume d'une pyramide
Dans l'espace rapporté à un repère orthonormé
 , on considère les points:
, on considère les points:
A de coordonnées (2 ; 0 ; 0), B de coordonnées (0 ; 3 ; 0) et C de coordonnées (0 ; 0 ; 1).
(2.4,4.5)(10.4,2)
%\psgrid
\psline(0,0)(8,0)(10.4,2)(10.4,4.5)(8,2.5)(8,0)
\psline(8,2.5)(0,2.5)(0,0)
\psline(0,2.5)(2.4,4.5)(10.4,4.5)
\psline[linestyle=dashed](0,0)(2.4,2)(2.4,4.5)
\psline[linestyle=dashed](2.4,2)(10.4,2)
\uput[dl](0,0){A}\uput[u](2.4,4.5){C}\uput[r](10.4,2){B}\uput[d](2.5,2){O}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex150321/2.png)
L'objectif de cet exercice est de calculer l'aire du triangle ABC.
(Bac général, spécialité mathématiques, 15 mars 2021)
(2.4,4.5)(10.4,2)
%\psgrid
\psline(0,0)(8,0)(10.4,2)(10.4,4.5)(8,2.5)(8,0)
\psline(8,2.5)(0,2.5)(0,0)
\psline(0,2.5)(2.4,4.5)(10.4,4.5)
\psline[linestyle=dashed](0,0)(2.4,2)(2.4,4.5)
\psline[linestyle=dashed](2.4,2)(10.4,2)
\rput[l](-.4,-.5){A(2;0;0)}
\rput[l](2.4,4.8){C(0;0;1)}
\rput[l](10.6,2){B(0;3;0)}
\uput[d](2.5,2){O}
\psline[linecolor=red,linewidth=1.4pt]{->}(2.4,2)(1.2,1)
\rput(1.5,1.8){\red$\vec{i}$}
\psline[linecolor=red,linewidth=1.4pt]{->}(2.4,2)(4.9,2)
\rput(3.4,1.5){\red$\vec{j}$}
\psline[linecolor=red,linewidth=1.4pt]{->}(2.4,2)(2.4,4.5)
\rput(2,3){\red$\vec{j}$}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex150321_c/1.png)
Cacher la correction
A de coordonnées (2 ; 0 ; 0), B de coordonnées (0 ; 3 ; 0) et C de coordonnées (0 ; 0 ; 1).
(2.4,4.5)(10.4,2)
%\psgrid
\psline(0,0)(8,0)(10.4,2)(10.4,4.5)(8,2.5)(8,0)
\psline(8,2.5)(0,2.5)(0,0)
\psline(0,2.5)(2.4,4.5)(10.4,4.5)
\psline[linestyle=dashed](0,0)(2.4,2)(2.4,4.5)
\psline[linestyle=dashed](2.4,2)(10.4,2)
\uput[dl](0,0){A}\uput[u](2.4,4.5){C}\uput[r](10.4,2){B}\uput[d](2.5,2){O}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex150321/2.png)
L'objectif de cet exercice est de calculer l'aire du triangle ABC.
-
- Montrer que le vecteur
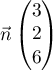 est normal au plan (ABC).
est normal au plan (ABC).
- En déduire qu'une équation cartésienne du plan (ABC) est :
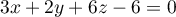 .
.
- Montrer que le vecteur
- On note
 la droite passant par O et orthogonale au plan (ABC).
la droite passant par O et orthogonale au plan (ABC).
- Déterminer une représentation paramétrique de la droite
 .
.
- Montrer que la droite
 coupe le plan (ABC) au point H
de coordonnées
coupe le plan (ABC) au point H
de coordonnées
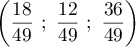 .
.
- Calculer la distance OH.
- Déterminer une représentation paramétrique de la droite
- On rappelle que le volume d'une pyramide est donné par:
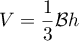 , où
, où 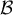 est l'aire d'une
base et
est l'aire d'une
base et 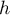 est la hauteur de la pyramide correspondant à cette base.
est la hauteur de la pyramide correspondant à cette base.
En calculant de deux façons différentes le volume de la pyramide OABC, déterminer l'aire du triangle ABC.
Correction exercice 7
(Bac général, spécialité mathématiques, 15 mars 2021)
(2.4,4.5)(10.4,2)
%\psgrid
\psline(0,0)(8,0)(10.4,2)(10.4,4.5)(8,2.5)(8,0)
\psline(8,2.5)(0,2.5)(0,0)
\psline(0,2.5)(2.4,4.5)(10.4,4.5)
\psline[linestyle=dashed](0,0)(2.4,2)(2.4,4.5)
\psline[linestyle=dashed](2.4,2)(10.4,2)
\rput[l](-.4,-.5){A(2;0;0)}
\rput[l](2.4,4.8){C(0;0;1)}
\rput[l](10.6,2){B(0;3;0)}
\uput[d](2.5,2){O}
\psline[linecolor=red,linewidth=1.4pt]{->}(2.4,2)(1.2,1)
\rput(1.5,1.8){\red$\vec{i}$}
\psline[linecolor=red,linewidth=1.4pt]{->}(2.4,2)(4.9,2)
\rput(3.4,1.5){\red$\vec{j}$}
\psline[linecolor=red,linewidth=1.4pt]{->}(2.4,2)(2.4,4.5)
\rput(2,3){\red$\vec{j}$}
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex150321_c/1.png)
-
- Pour montrer que le vecteur
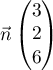 est normal au plan (ABC),
il suffit de démontrer que ce vecteur est orthogonal à deux vecteurs
directeurs du plan (ABC), par exemple
est normal au plan (ABC),
il suffit de démontrer que ce vecteur est orthogonal à deux vecteurs
directeurs du plan (ABC), par exemple  et
et  .
On a
.
On a 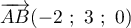 donc
donc
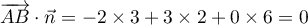 et ainsi
et ainsi 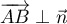 .
.
De même,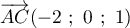 donc
donc
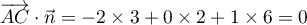 et ainsi, aussi,
et ainsi, aussi, 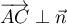 .
On en déduit que le vecteur
.
On en déduit que le vecteur 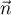 est normal au plan (ABC).
est normal au plan (ABC).
-
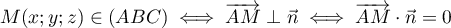 .
.
Or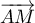 a pour coordonnées
a pour coordonnées 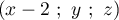 .
.
et donc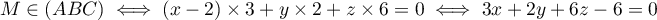
Le plan (ABC) a donc pour équation cartésienne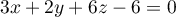 .
.
- Pour montrer que le vecteur
-
-
La droite
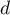 est orthogonale au plan (ABC) donc elle a pour vecteur directeur le vecteur
est orthogonale au plan (ABC) donc elle a pour vecteur directeur le vecteur 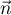 normal à (ABC).
normal à (ABC).
De plus elle passe par le point O de coordonnées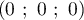 .
.
Une représentation paramétrique de la droite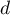 est donc
est donc
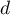
- La droite
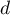 est orthogonale au plan (ABC),
et donc elle le coupe en un point H.
Soit
est orthogonale au plan (ABC),
et donc elle le coupe en un point H.
Soit 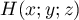 alors on a
alors on a
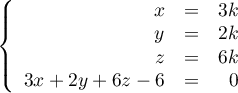
Donc, en substituant dans la troisième équation, on obtient
![\[\begin{array}{ll}&3\tm3k+2\tm 2k+6\tm 6k-6 = 0\\[.3em]
\iff& 9k+4k+36k=6\\
\iff& k=\dfrac{6}{49}\enar\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex150321_c/25.png)
On en déduit que
![\[\la\begin{array}{rcrcr}
x&=&3k&=&\dfrac{18}{49}\\[.8em]
y&=&2k&=&\dfrac{12}{49}\\[.8em]
z&=&6k&=&\dfrac{36}{49}\enar\right.\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex150321_c/26.png)
et on a donc trouvé les coordonnées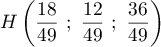 .
.
- On calcule alors directement
![\[\begin{array}{ll}
OH^2&=\left( x_{\text H}-x_{\text O}\rp^2 +
\left( y_{\text H}-y_{\text O}\rp^2 + \left( z_{\text H}-z_{\text O}\rp^2 \\[.6em]
&=\lp\dfrac{18}{49}\rp^2+\lp\dfrac{12}{49}\rp^2+\lp\dfrac{36}{49}\rp^2\\[1em]
&= \dfrac{18^2+12^2+36^2}{49^2} = \dfrac{1764}{49^2}
\enar\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex150321_c/28.png)
On obtient donc la distance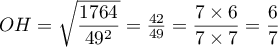 .
.
-
La droite
-
- On peut prendre le triangle OAB pour base de la pyramide OABC,
la hauteur est alors OC, et le volume
![\[\mathcal{V}=\dfrac{1}{3}\times \mathcal{B}\times OC\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex150321_c/30.png)
avec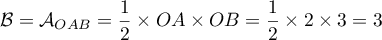 et
et  .
.
On obtient donc le volume
![\[\mathcal{V}=\dfrac{1}{3}\times 3 \times 1= 1\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex150321_c/33.png)
- On peut aussi prendre le triangle ABC pour base de la pyramide OABC,
la hauteur est alors OH, et le volume est
![\[\mathcal{V}=\dfrac13\times \mathcal{B}'\times OH\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex150321_c/34.png)
avec est l'aire du triangle ABC.
est l'aire du triangle ABC.
On a ici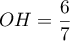 et
et  donc
donc
![\[\mathcal{V}=1=\dfrac13\times \mathcal{B}' \times \dfrac{6}{7}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex150321_c/38.png)
d'où on déduit que
![\[\mathcal{B}'=\mathcal{A}_{ABC}==\dfrac{49}{14}= \dfrac72\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex150321_c/39.png)
.
- On peut prendre le triangle OAB pour base de la pyramide OABC,
la hauteur est alors OC, et le volume
Cacher la correction
Exercice 8: Bac 2021 - Orthogonalité dans l'espace et minimisation d'une distance et volume d'une pyramide
Dans un repère orthonormé  on considère
on considère
Le but de cet exercice est de déterminer le point de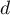 le plus proche du point A et d'étudier quelques propriétés de ce point.
le plus proche du point A et d'étudier quelques propriétés de ce point.
On pourra s'appuyer sur la figure ci-contre pour raisonner au fur et à mesure des questions.
![\[\psset{unit=1.6cm}
\begin{pspicture}(-1.9,-2)(4,2.5)
\psline{->}(-1.7,0)(4,0)
\psline{->}(0,0)(-1,-1.5)
\psline{->}(0,-1.8)(0,2.5)
\rput(-1.2,-1.5){$x$}
\rput(3.95,.2){$y$}
\rput(-.15,2.4){$z$}
\psline(-1,.08)(-1,-.08)\psline(1,.08)(1,-.08)\psline(2,.08)(2,-.08)\psline(3,.08)(3,-.08)
\psline(-.08,-1)(.08,-1)\psline(-.08,1)(.08,1)\psline(-.08,2)(.08,2)
\psline(-.41,-.5)(-.25,-.5)
\psline(-.73,-1)(-.58,-1)
% rep\`ere
\psline[arrowsize=7pt,linewidth=1.2pt]{->}(0,0)(1,0)
\psline[arrowsize=7pt,linewidth=1.2pt]{->}(0,0)(0,1)
\psline[arrowsize=7pt,linewidth=1.2pt]{->}(0,0)(-.35,-.5)
\rput(-.5,-.4){$\vec{i}$}
\rput(-.2,.7){$\vec{k}$}
\rput(.8,.25){$\vec{j}$}
%droite d
\psline(-1,1)(2,-2)\rput(.25,-.5){$\vec{u}$}
\psline[arrowsize=8pt]{->}(0,0)(.5,-.5)
%
\psline(0,0)(2.5,1.5)(2.5,-.5)(1.2,-1.2)
\rput(2.65,1.65){A}
\psline[linestyle=dashed](0,0)(2.5,-.5)
\rput(2.65,-.65){A'}
\psline(2.5,1.5)(1.2,-1.2)
\rput(1,-1.3){$M_0$}
%\psline(-4,-.5)(4,-.5)
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex070621/10.png)
(Bac général, spécialité mathématiques, métropole, 7 juin 2021)
Cacher la correction
- le point A de coordonnées (1 ; 3 ; 2),
- le vecteur
 de coordonnées
de coordonnées 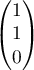
- la droite
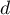 passant par l'origine O du repère et admettant pour vecteur directeur
passant par l'origine O du repère et admettant pour vecteur directeur 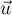 .
.
Le but de cet exercice est de déterminer le point de
On pourra s'appuyer sur la figure ci-contre pour raisonner au fur et à mesure des questions.
![\[\psset{unit=1.6cm}
\begin{pspicture}(-1.9,-2)(4,2.5)
\psline{->}(-1.7,0)(4,0)
\psline{->}(0,0)(-1,-1.5)
\psline{->}(0,-1.8)(0,2.5)
\rput(-1.2,-1.5){$x$}
\rput(3.95,.2){$y$}
\rput(-.15,2.4){$z$}
\psline(-1,.08)(-1,-.08)\psline(1,.08)(1,-.08)\psline(2,.08)(2,-.08)\psline(3,.08)(3,-.08)
\psline(-.08,-1)(.08,-1)\psline(-.08,1)(.08,1)\psline(-.08,2)(.08,2)
\psline(-.41,-.5)(-.25,-.5)
\psline(-.73,-1)(-.58,-1)
% rep\`ere
\psline[arrowsize=7pt,linewidth=1.2pt]{->}(0,0)(1,0)
\psline[arrowsize=7pt,linewidth=1.2pt]{->}(0,0)(0,1)
\psline[arrowsize=7pt,linewidth=1.2pt]{->}(0,0)(-.35,-.5)
\rput(-.5,-.4){$\vec{i}$}
\rput(-.2,.7){$\vec{k}$}
\rput(.8,.25){$\vec{j}$}
%droite d
\psline(-1,1)(2,-2)\rput(.25,-.5){$\vec{u}$}
\psline[arrowsize=8pt]{->}(0,0)(.5,-.5)
%
\psline(0,0)(2.5,1.5)(2.5,-.5)(1.2,-1.2)
\rput(2.65,1.65){A}
\psline[linestyle=dashed](0,0)(2.5,-.5)
\rput(2.65,-.65){A'}
\psline(2.5,1.5)(1.2,-1.2)
\rput(1,-1.3){$M_0$}
%\psline(-4,-.5)(4,-.5)
\end{pspicture}\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex070621/10.png)
- Déterminer une représentation paramétrique de la droite
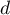 .
.
- Soit
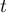 un nombre réel quelconque, et
un nombre réel quelconque, et 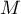 un point de la droite
un point de la droite 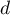 , le point
, le point 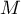 ayant pour coordonnées
ayant pour coordonnées 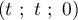 .
.
- On note AM la distance entre les points A et M.
Démontrer que:
![\[AM^2 = 2t^2 - 8t+ 14.\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex070621/19.png)
- Démontrer que le point
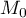 de coordonnées
de coordonnées 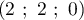 est le point de la droite
est le point de la droite 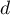 pour lequel la distance
pour lequel la distance 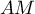 est minimale.
est minimale.
On admettra que la distance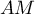 est minimale
lorsque son carré
est minimale
lorsque son carré 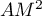 est minimal.
est minimal.
- On note AM la distance entre les points A et M.
Démontrer que:
- Démontrer que les droites
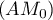 et
et 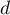 sont orthogonales.
sont orthogonales.
- On appelle
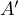 le projeté orthogonal du point
le projeté orthogonal du point 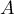 sur le plan
d'équation cartésienne
sur le plan
d'équation cartésienne 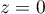 .
Le point
.
Le point  admet donc pour coordonnées
admet donc pour coordonnées 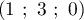 .
.
Démontrer que le point est le point du plan
est le point du plan 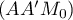 le plus proche du point O, origine du repère.
le plus proche du point O, origine du repère.
- Calculer le volume de la pyramide
 .
.
On rappelle que le volume d'une pyramide est donné par: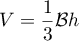 , où
, où  est l'aire
d'une base et
est l'aire
d'une base et 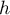 est la hauteur de la pyramide correspondant
à cette base.
est la hauteur de la pyramide correspondant
à cette base.
Correction exercice 8
(Bac général, spécialité mathématiques, métropole, 7 juin 2021)
-
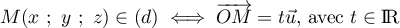 , soit :
, soit :
![\[\left\{\begin{array}{l c l}
x&=&t\\
y&=&t\\
z&=&0
\end{array}\right., \, t \in \R\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex070621_c/2.png)
-
- De
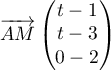 ,
on calcule:
,
on calcule:
![\[\begin{array}{ll}AM^2 &= (t - 1)^2 + (t - 3)^2 + (- 2)^2 \\[.3em]
&= t^2 + 1 - 2t + t^2 + 9 - 6t + 4 \\[.3em]
&= 2t^2 - 8t+ 14\enar\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex070621_c/4.png)
- L'expression précédente est une expression du second degré.
On peut soit étudier les variations (dérivée, signe, ...)
soit se rappeler que le sommet de la parabole est en
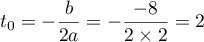 .
.
On a alors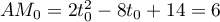 ,
et donc la plus petite distance est
,
et donc la plus petite distance est
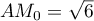 avec
avec 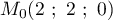 .
.
- De
- On a
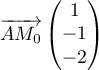 et
et 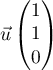 est un vecteur directeur
de
est un vecteur directeur
de 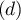 .
.
On a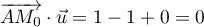 : les vecteurs sont orthogonaux donc les droites
: les vecteurs sont orthogonaux donc les droites  et
et 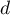 sont orthogonales.
sont orthogonales.
-
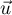 est orthogonal au plan horizontal d'équation
est orthogonal au plan horizontal d'équation 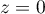 .
Comme A
.
Comme A et
et  appartiennent à ce plan le vecteur
appartiennent à ce plan le vecteur 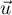 est orthogonal au vecteur
est orthogonal au vecteur 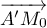 .
.
Donc le vecteur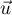 est orthogonal à deux vecteurs non colinéaires
du plan
est orthogonal à deux vecteurs non colinéaires
du plan 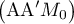 ,donc la droite
,donc la droite 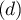 est orthogonale
au plan
est orthogonale
au plan
 .
Le point
.
Le point  est donc le projeté orthogonal de O
sur le plan
est donc le projeté orthogonal de O
sur le plan  , donc O
, donc O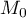 est la distance
la plus courte du point O au plan
est la distance
la plus courte du point O au plan 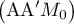 .
.
- On peut prendre la base
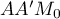 qui est un triangle rectangle en
qui est un triangle rectangle en 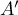 ,
avec
,
avec 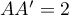
et donc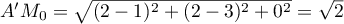 .
.
On a donc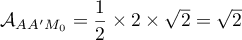 .
.
D'autre part, la hauteur correspondante est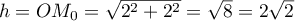 .
.
On obtient finalement
![\[V = \left( AA'M_0\right) = \dfrac{\sqrt2 \times 2\sqrt{2}}{3} = \dfrac43\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex070621_c/35.png)
Cacher la correction
Exercice 9: Bac 2018, Pondichéry - Droite, plan, intersection
Dans l'espace muni du repère orthonormé 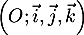 d'unité 1 cm, on considère les points
A, B, C et D de coordonnées respectives (2 ; 1 ; 4), (4 ; -1 ; 0), (0 ; 3 ; 2) et (4 ; 3 ; -2).
d'unité 1 cm, on considère les points
A, B, C et D de coordonnées respectives (2 ; 1 ; 4), (4 ; -1 ; 0), (0 ; 3 ; 2) et (4 ; 3 ; -2).
Cacher la correction
- Déterminer une représentation paramétrique de la droite (CD).
- Soit M un point de la droite (CD).
- Déterminer les coordonnées du point M tel que la distance BM soit minimale.
- On note H le point de la droite (CD) ayant pour coordonnées (3 ; 3 ; - 1). Vérifier que les droites (BH) et (CD) sont perpendiculaires.
- Montrer que l'aire du triangle BCD est égale à
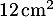 .
.
-
- Démontrer que le vecteur
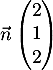 est un vecteur normal au plan (BCD).
est un vecteur normal au plan (BCD).
- Déterminer une équation cartésienne du plan (BCD).
- Déterminer une représentation paramétrique de la droite
 passant par A et orthogonale
au plan (BCD).
passant par A et orthogonale
au plan (BCD).
- Démontrer que le point I, intersection de la droite
 et du plan (BCD) a pour
coordonnées
et du plan (BCD) a pour
coordonnées 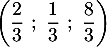 .
.
- Démontrer que le vecteur
- Calculer le volume du tétraèdre ABCD.
Correction exercice 9
-
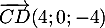 est un vecteur directeur de la droite
est un vecteur directeur de la droite  ,
d'où la représentation paramétrique
,
d'où la représentation paramétrique
![\[(CD):\la\begin{array}{ll}x=4t\\y=3\\z=2-4t\enar\right.\,, \ t\in\R\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex2018_c/3.png)
- Soit M un point de la droite (CD).
-
 est minimale si et seulement si
est minimale si et seulement si  est le projeté orthogonal
de
est le projeté orthogonal
de 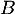 sur la droite
sur la droite 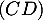 :
donc
:
donc 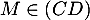 et
et 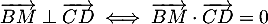 .
.
Soit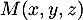 , alors il existe
, alors il existe 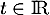 tel que
tel que
![\[M\in(CD)\iff\la\begin{array}{ll}x=4t\\y=3\\z=2-4t\enar\right.
\quad\text{ et } \quad
\begin{array}[t]{ll}\overrightarrow{BM}\cdot\overrightarrow{CD}&=4(x-4)+0(y+1)+(-4)(z-0)=0 \\
&\iff 4x-4z=16\end{array}
\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex2018_c/12.png)
On doit donc avoir
![\[4x-4z=4(4t)-4(2-4t)=16\iff 32t-8=16\iff t=\dfrac{24}{32}=\dfrac34\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex2018_c/13.png)
et donc finalement,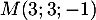 .
.
-
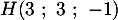 donc
donc 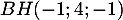 et alors
et alors
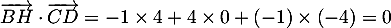 ,
ce qui montre que les droites
,
ce qui montre que les droites 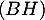 et
et 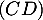 sont orthogonales.
sont orthogonales.
De plus, on sait que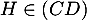 , donc que ces deux droites sont sécantes
en
, donc que ces deux droites sont sécantes
en  .
.
On en déduit donc que ces deux droites et
et  sont bien
perpendiculaires.
sont bien
perpendiculaires.
- D'après ce qui précède,
 est la hauteur issue de
est la hauteur issue de  dans
dans
 , et donc
, et donc
![\[\mathcal{A}_{BCD} = \dfrac12\times CD \times BH
= \dfrac12\tm\sqrt{32}\tm\sqrt{18}= \sqrt{144}= 12\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex2018_c/27.png)
-
-
- On a
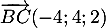 et
et 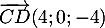 , d'où
, d'où
![\[\begin{array}{lcl}
\vec{n}\cdot\overrightarrow{BC}&=&2\tm(-4)+1\tm4+2\tm2=0\\[.4em]
\vec{n}\cdot\overrightarrow{CD}&=&2\tm(4)+1\tm0+2\tm(-4)=0
\enar\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex2018_c/30.png)
Ainsi, le vecteur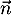 est orthogonal à deux vecteurs non colinéaires
du plan
est orthogonal à deux vecteurs non colinéaires
du plan 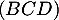 et ainsi il est orthogonal à tous les vecteurs de ce plan,
c'est-à-dire orthogonal au plan
et ainsi il est orthogonal à tous les vecteurs de ce plan,
c'est-à-dire orthogonal au plan 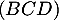 .
.
- On déduit de ce qui précède qu'une équation cartésienne du plan
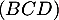 s'écrit sous la forme
s'écrit sous la forme
![\[2x+y+2z+d=0\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex2018_c/35.png)
avec de plus, par exemple,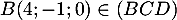 donc
donc  ,
d'où l'équation
,
d'où l'équation
![\[2x+y+2z-7=0\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex2018_c/38.png)
- La droite
 est orthogonale au plan
est orthogonale au plan  ) et donc
) et donc 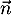 en
est un vecteur directeur, avec de plus
en
est un vecteur directeur, avec de plus 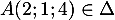 , d'où
une représentation paramétrique
, d'où
une représentation paramétrique
![\[\Delta:\la\begin{array}{ll}x=2+2t\\y=1+t\\z=4+2t\enar\right.\ , \ t\in\R\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex2018_c/43.png)
- Soit
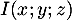 , intersection de la droite
, intersection de la droite  et du plan
et du plan  ,
alors
d'une part
,
alors
d'une part 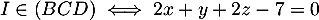 .
.
D'autre part, comme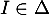 , et d'après la question précèdente,
il existe un réel
, et d'après la question précèdente,
il existe un réel  tel que les coordonnées de
tel que les coordonnées de  vérifient les équations
paramétriques de
vérifient les équations
paramétriques de  .
.
On a donc
![\[2(2+2t)+(1+t)+2(4+2t)-7=0 \iff 9t+6=0\iff t=-\dfrac69=-\dfrac23\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex2018_c/52.png)
et on trouve alors les coordonnées
![\[\la\begin{array}{ll}x=2+2\lp-\dfrac23\rp=\dfrac23\\
y=1+\lp-\dfrac23\rp=\dfrac13\\
z=4+2\lp-\dfrac23\rp=\dfrac83\enar\right.\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex2018_c/53.png)
qui sont les coordonnées recherchées.
- On a
- Comme
 est perpendiculaire au plan
est perpendiculaire au plan  en
en  et passe par
et passe par  ,
on en déduit que
,
on en déduit que  est la hauteur du tétraèdre
est la hauteur du tétraèdre  de base
de base  ,
et donc
,
et donc
![\[\mathcal{V}_{ABCD} = \dfrac13\times AI\times \mathcal{A}_{ABCD}
=\dfrac13\times AI\times12\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex2018_c/61.png)
avec
![\[\begin{array}{ll}AI&=\sqrt{\lp\dfrac23-2\rp^2+\lp\dfrac13-1\rp^2+\lp\dfrac83-4\rp^2}\\[1.4em]
&=\sqrt{\dfrac{4^2+2^2+4^2}{3^2}}=\sqrt{\dfrac{36}{3^2}}=\dfrac63=2
\enar\]](/Generateur-Devoirs/TS/ChapGeomSpace/ex2018_c/62.png)
d'où le volume du tétraèdre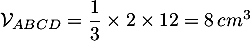
Cacher la correction
Exercice 10: Bac 2015, Nouvelle Calédonie - Droites perpendiculaires dans l'espace
L'espace est rapporté au repère orthonormé
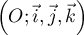 .
On désigne par
.
On désigne par  l'ensemble des
nombres réels.
l'ensemble des
nombres réels.
On rappelle que deux droites de l'espace sont dites perpendiculaires si et seulement si elles sont orthogonales et sécantes.
Soient le point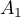 de coordonnées
de coordonnées 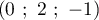 et le vecteur
et le vecteur
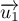 de coordonnées
de coordonnées 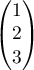 .
.
On appelle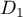 la droite passant par
la droite passant par 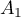 et de vecteur directeur
et de vecteur directeur
 .
.
On appelle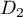 la droite qui admet pour représentation paramétrique
la droite qui admet pour représentation paramétrique
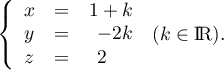
Le but de l'exercice est de prouver l'existence d'une droite perpendiculaire à la fois à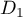 et
et  .
.
Cacher la correction
On rappelle que deux droites de l'espace sont dites perpendiculaires si et seulement si elles sont orthogonales et sécantes.
Soient le point
On appelle
On appelle
Le but de l'exercice est de prouver l'existence d'une droite perpendiculaire à la fois à
-
- Donner une représentation paramétrique de
 .
.
- Donner un vecteur directeur de
 (on le notera :
(on le notera : 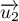 ).
).
- Le point
 appartient-il à
appartient-il à 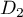 ?
?
- Donner une représentation paramétrique de
- Démontrer que les droites
 et
et 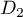 sont non coplanaires.
sont non coplanaires.
- Soit le vecteur
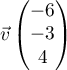 .
On définit la droite
.
On définit la droite  passant par
passant par 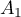 et de vecteur directeur
et de vecteur directeur 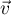 et la droite
et la droite 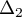 passant
par
passant
par  et parallèle à
et parallèle à  .
Justifier que les droites
.
Justifier que les droites  et
et  sont
perpendiculaires.
sont
perpendiculaires.
Dans la suite, on admettra que les droites et
et  sont perpendiculaires.
sont perpendiculaires.
- Soit
 le plan défini par les droites
le plan défini par les droites  et
et  et
et
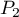 le plan défini par les droites
le plan défini par les droites  et
et  .
.
- Soit le vecteur
 .
Vérifier que
.
Vérifier que  est un vecteur normal au plan
est un vecteur normal au plan  .
.
- Montrer que
 et
et  ne sont pas parallèles.
ne sont pas parallèles.
- Soit le vecteur
- Soit
 la droite d'intersection des plans
la droite d'intersection des plans  et
et
 . On admettra que le vecteur
. On admettra que le vecteur 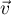 est un vecteur directeur
de
est un vecteur directeur
de  .
Utiliser les questions précédentes pour prouver qu'il existe une
droite de l'espace perpendiculaire à la fois à
.
Utiliser les questions précédentes pour prouver qu'il existe une
droite de l'espace perpendiculaire à la fois à 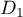 et à
et à 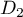 .
.
Correction exercice 10
-
- Une représentation paramétrique de
 s'obtient en
traduisant l'égalité
s'obtient en
traduisant l'égalité 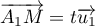 avec
avec 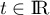 soit:
soit:
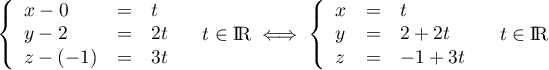 .
.
- Dans la représentation paramétrique, on reconnait qu'un
vecteur directeur de
 est
est
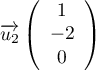 .
.
-
 qui a une solution
qui a une solution  .
.
Le point appartient à
appartient à  .
.
- Une représentation paramétrique de
- Les vecteurs directeurs de
 et de
et de  ne sont
pas colinéaires, donc les droites ne sont pas
parallèles.
Elles sont sécantes s'il existe des réels
ne sont
pas colinéaires, donc les droites ne sont pas
parallèles.
Elles sont sécantes s'il existe des réels  et
et 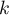 tels que:
tels que:
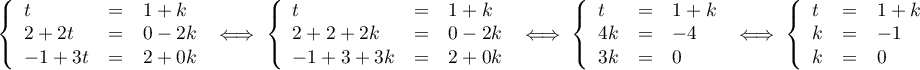 Ce système n'a pas de solution donc il n'existe pas de point commun
aux deux droites, elles ne sont donc pas coplanaires.
Ce système n'a pas de solution donc il n'existe pas de point commun
aux deux droites, elles ne sont donc pas coplanaires.
- Les droites
 et
et  contiennent le point
contiennent le point
 . Pour montrer qu'elles sont perpendiculaires il suffit de
montrer que deux de leurs vecteurs directeurs sont orthogonaux :
. Pour montrer qu'elles sont perpendiculaires il suffit de
montrer que deux de leurs vecteurs directeurs sont orthogonaux :
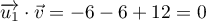 .
Ainsi, les droites
.
Ainsi, les droites  et
et  sont perpendiculaires.
sont perpendiculaires.
- Les droites
 et
et  sont aussi perpendiculaires
sont aussi perpendiculaires
-
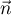 est un vecteur normal au plan
est un vecteur normal au plan  s'il est
orthogonal aux deux vecteurs non colinéaires et non nuls de ce
plan
s'il est
orthogonal aux deux vecteurs non colinéaires et non nuls de ce
plan 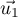 et
et 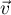 ; or
; or
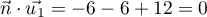
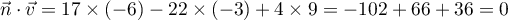
Le vecteur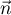 est orthogonal a deux vecteurs non colinéaires du
plan
est orthogonal a deux vecteurs non colinéaires du
plan 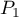 .
Il est par conséquent normal à ce plan.
.
Il est par conséquent normal à ce plan.
- Si
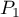 et
et 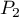 sont parallèles,
sont parallèles,  vecteur normal au
plan
vecteur normal au
plan  est aussi un vecteur normal au plan
est aussi un vecteur normal au plan  ; il est
donc orthogonal à tout vecteur non nul du plan
; il est
donc orthogonal à tout vecteur non nul du plan  comme
comme  et
et  .
On a bien
.
On a bien 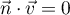 ,
mais
,
mais 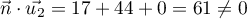 .
.
Donc n'est pas normal au plan
n'est pas normal au plan  et les deux plans
et les deux plans
 et
et  ne sont pas parallèles.
ne sont pas parallèles.
-
-
 est parallèle à
est parallèle à  et
et  lesquelles
sont respectivement perpendiculaire à
lesquelles
sont respectivement perpendiculaire à  et
et  .
.
Par conséquent la droite est orthogonale aux droites
est orthogonale aux droites  et
et  .
.
Or cette droite appartient au plan et au plan
et au plan  . Elle est
donc perpendiculaire aux droites
. Elle est
donc perpendiculaire aux droites  et
et  .
Il existe donc une droite de l'espace perpendiculaire à la droite
.
Il existe donc une droite de l'espace perpendiculaire à la droite
 et à
et à 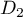 : c'est la droite
: c'est la droite 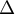 .
.
Cacher la correction
Exercice 11: Bac 2015 - Géométrie dans l'espace
Dans un repère orthonormé (O, I, J, K) d'unité 1 cm, on considère les points
Un point
Un point
À l'instant
On note
On admet que
Les questions 1 et 2 sont indépendantes.
-
- La droite
 est parallèle à l'un des axes
est parallèle à l'un des axes 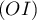 ,
, 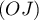 ou
ou  . Lequel ?
. Lequel ?
- La droite
 se trouve dans un plan
se trouve dans un plan 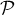 parallèle à l'un des plans
parallèle à l'un des plans  ,
, 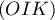 ou
ou  .
Lequel ? On donnera une équation de ce plan
.
Lequel ? On donnera une équation de ce plan  .
.
- Vérifier que la droite
 , orthogonale au plan
, orthogonale au plan  , coupe ce plan au point
, coupe ce plan au point  .
.
- Les droites
 et
et  sont-elles sécantes ?
sont-elles sécantes ?
- La droite
-
- Montrer que
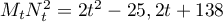 .
.
- À quel instant
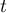 la longueur
la longueur  est-elle minimale?
est-elle minimale?
- Montrer que
Correction exercice 11
-
- Un vecteur directeur de la droite
 est
est 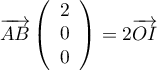 .
La droite
.
La droite  est donc parallèle à l'axe
est donc parallèle à l'axe  .
.
-
 est un
vecteur directeur de la droite
est un
vecteur directeur de la droite  qui est donc incluse dans un
plan parallèle à
qui est donc incluse dans un
plan parallèle à 
Comme le plan
le plan  a pour équation cartésienne
a pour équation cartésienne 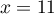 .
.
- On a
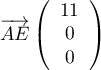 et
et
 , ce qui montre que ces vecteurs
sont colinéaires, et ainsi que
, ce qui montre que ces vecteurs
sont colinéaires, et ainsi que  est un point de la droite
est un point de la droite
 .
.
De plus , et donc
, et donc  .
.
Ainsi, est bien le point d'intersection de
est bien le point d'intersection de 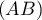 et de
et de  .
.
Remarque: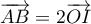 , donc
, donc  ,
et comme
,
et comme  est parallèle au plan
est parallèle au plan  ,
,
 est bien orthogonale au plan
est bien orthogonale au plan  .
Cette justification n'était par contre pas demandée…
.
Cette justification n'était par contre pas demandée…
-
 est incluse dans
est incluse dans  , et
, et  coupe
coupe
 en
en  .
.
Ainsi, si et
et  sont sécantes, elles le sont
nécessairement au point
sont sécantes, elles le sont
nécessairement au point  .
.
Or, n'est pas colinéaire à
n'est pas colinéaire à
 , ce qui montre que
, ce qui montre que  .
.
Ainsi, et
et  ne sont pas sécantes.
ne sont pas sécantes.
Autre méthode. On peut aussi chercher directement l'éventuelle intersection des deux droites à l'aide de leur représentation paramétrique:

On cherche alors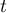 et
et  tels que
tels que
 .
Or ce système n'a pas de solution, et donc
.
Or ce système n'a pas de solution, et donc  et
et  pas
d'intersection et ne sont donc pas sécantes.
pas
d'intersection et ne sont donc pas sécantes.
- Un vecteur directeur de la droite
-
-
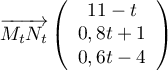 donc
donc 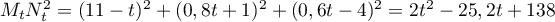 .
.
-
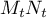 est positif, donc est minimale quand son carré est minimal.
On définit la fonction
est positif, donc est minimale quand son carré est minimal.
On définit la fonction 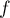 sur
sur 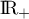 par l'expression
par l'expression
 .
.
 est une fonction du second degré avec
est une fonction du second degré avec
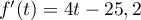 .
.
Ainsi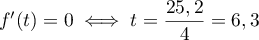 , et
, et 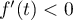 donc
donc 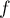 est décroissante pour
est décroissante pour  , et
, et 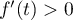 donc
donc 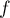 croissante
pour
croissante
pour 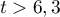 .
.
Ainsi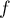 , donc
, donc  , admet un minimum en
, admet un minimum en 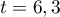 .
.
-
Cacher la correction
Exercice 12: Bac 2014 - Géométrie dans l'espace, dans un tétraèdre…
Dans l'espace, on considère un tétraèdre 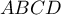 dont les faces
dont les faces 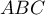 ,
,
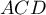 et
et 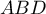 sont des triangles rectangles et isocèles en A.
On désigne par
sont des triangles rectangles et isocèles en A.
On désigne par 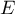 ,
, 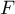 et
et 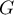 les milieux respectifs des côtés
les milieux respectifs des côtés
![$[AB]](/Generateur-Devoirs/TS/ChapGeomSpace/ex114/8.png) ,
, ![$[BC]](/Generateur-Devoirs/TS/ChapGeomSpace/ex114/9.png) et
et ![$[CA]](/Generateur-Devoirs/TS/ChapGeomSpace/ex114/10.png) .
.
On choisit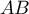 pour unité de longueur et on se place dans le repère
orthonormé
pour unité de longueur et on se place dans le repère
orthonormé 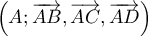 de l'espace.
de l'espace.
Tout d'abord, une figure :
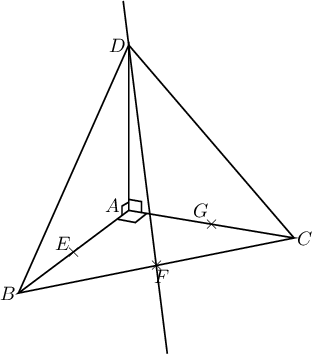
Cacher la correction
On choisit
- On désigne par
 le plan qui passe par A et qui est
orthogonal à la droite (DF).
le plan qui passe par A et qui est
orthogonal à la droite (DF).
On note H le point d'intersection du plan et de la droite (DF).
et de la droite (DF).
- Donner les coordonnées des points D et F.
- Donner une représentation paramétrique de la droite (DF).
- Déterminer une équation cartésienne du plan
 .
.
- Calculer les coordonnées du point H.
- Démontrer que l'angle
 est un angle droit.
est un angle droit.
- On désigne par
 un point de la droite
un point de la droite 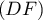 et par
et par 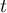 le
réel tel que
le
réel tel que 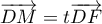 .
On note
.
On note 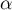 la mesure en radians de l'angle géométrique
la mesure en radians de l'angle géométrique
 .
.
Le but de cette question est de déterminer la position du point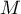 pour que
pour que 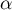 soit maximale.
soit maximale.
- Démontrer que
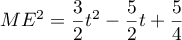 .
.
- Démontrer que le triangle
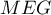 est isocèle en
est isocèle en  .
En déduire que
.
En déduire que 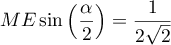 .
.
- Justifier que
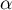 est maximale si et seulement si
est maximale si et seulement si
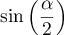 est maximal.
est maximal.
En déduire que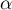 est maximale si et seulement si
est maximale si et seulement si 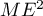 est minimal.
est minimal.
- Conclure.
- Démontrer que
Correction exercice 12
Tout d'abord, une figure :

-
- On a
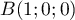 ,
, 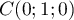 , et
, et 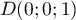 , pour les
coordonnées des points directement liés au repère, et alors
, pour les
coordonnées des points directement liés au repère, et alors
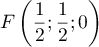 puisque
puisque 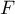 est le milieu de
est le milieu de
![$[BC]](/Generateur-Devoirs/TS/ChapGeomSpace/ex114_c/7.png) .
.
- Une représentation paramétrique de
 est donnée par
est donnée par
 où
où  est un point de la droite
de paramètre
est un point de la droite
de paramètre  , et
, et
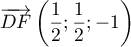 est un vecteur
directeur de la droite.
Cette relation se réécrit sous la forme de la représentation
paramétrique:
est un vecteur
directeur de la droite.
Cette relation se réécrit sous la forme de la représentation
paramétrique:
![$ \la\begin{array}{l}
x=\dfrac{1}{2}t\\[0.3cm]
y = \dfrac{1}{2}t\\[0.3cm]
z = 1 - t\enar\right. t \in \R](/Generateur-Devoirs/TS/ChapGeomSpace/ex114_c/13.png) .
.
- Le plan
 est orthogonal à
est orthogonal à 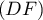 , donc
, donc
 est un vecteur normal à
est un vecteur normal à  et une équation
cartésienne de
et une équation
cartésienne de 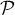 est
est
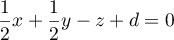 où
où  est un réel.
est un réel.
De plus, on sait que , et donc que
, et donc que
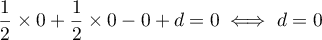 .
.
Ainsi, une équation cartésienne de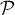 est
est
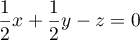
- Le point
 est un point de
est un point de 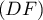 et de
et de 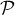 ,
donc ses coordonnées sont celles d'un point de paramètre
,
donc ses coordonnées sont celles d'un point de paramètre 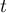 dans
la représentation paramétrique, et qui vérifient également l'équation
du plan: il existe
dans
la représentation paramétrique, et qui vérifient également l'équation
du plan: il existe 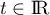 tel que:
tel que:
![$ \la\begin{array}{l}
x=\dfrac{1}{2}t\\[0.3cm]
y = \dfrac{1}{2}t\\[0.3cm]
z = 1 - t\\
\enar\right.](/Generateur-Devoirs/TS/ChapGeomSpace/ex114_c/30.png) et
et 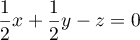 .
.
En substituant les expressions de ,
,  et
et  en fonction du
paramètre
en fonction du
paramètre  dans l'équation de
dans l'équation de 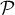 , on obtient:
, on obtient:
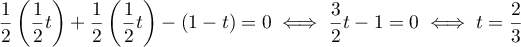
Ainsi, a pour coordonnées
a pour coordonnées
![$ \la\begin{array}{l}
x=\dfrac{1}{2}t=\dfrac12\dfrac23=\dfrac13\\[0.3cm]
y = \dfrac{1}{2}t=\dfrac12\dfrac23=\dfrac13\\[0.3cm]
z = 1 - t=1-\dfrac23=\dfrac13
\enar\right.](/Generateur-Devoirs/TS/ChapGeomSpace/ex114_c/39.png) ,
c'est à dire:
,
c'est à dire:  .
.
- Les coordonnées des vecteurs
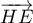 et
et 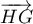 sont:
sont:
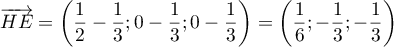 et
et
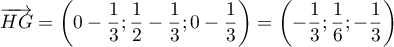 .
.
Comme on travaille avec un repère orthonormé, le produit scalaire des deux vecteurs peut être obtenu avec ces coordonnées, et on a: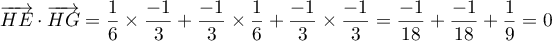 ,
ce qui montre que les vecteurs
,
ce qui montre que les vecteurs 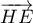 et
et  sont
orthogonaux, et donc que l'angle
sont
orthogonaux, et donc que l'angle  est droit.
est droit.
- On a
- On reconnaît dans le point
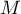 décrit, le point de paramètre
décrit, le point de paramètre 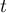 dans la représentation paramétrique de la droite
dans la représentation paramétrique de la droite 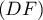 donnée à la
question 1. b..
donnée à la
question 1. b..
- Le point
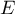 est le milieu du segment
est le milieu du segment ![$[AB]](/Generateur-Devoirs/TS/ChapGeomSpace/ex114_c/53.png) , donc ses
coordonnées sont
, donc ses
coordonnées sont 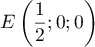 et le
vecteur
et le
vecteur 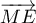 a pour coordonnées:
a pour coordonnées:
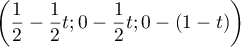 ,
soit
,
soit 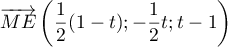 .
.
On a donc
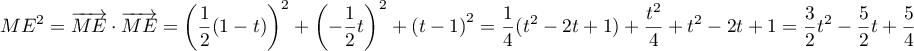
- On procède de façon analogue pour calculer la longueur
 :
Le point
:
Le point  est le milieu du segment
est le milieu du segment ![$[AC]](/Generateur-Devoirs/TS/ChapGeomSpace/ex114_c/61.png) , donc ses coordonnées
sont
, donc ses coordonnées
sont 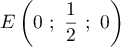 donc le vecteur
donc le vecteur 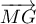 a pour coordonnées:
a pour coordonnées:
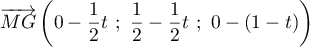 , soit
, soit 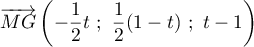 .
.
On a donc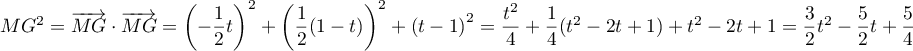 .
.
On a donc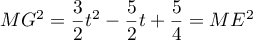 ,
et, comme
,
et, comme  et
et  sont des longueurs, donc des nombres
positifs, on a bien
sont des longueurs, donc des nombres
positifs, on a bien  et le triangle
et le triangle 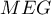 est isocèle.
est isocèle.
Dans le plan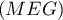 , on a la situation:
, on a la situation:
(0,3)
\psline(0,0.3)(0.3,0.3)(0.3,0)
\psarc(0,3){0.65}{245}{270}
\rput(-0.25,2){$\frac{\alpha}{2}$}
\rput(0,-0.2){$I$}
\end{pspicture}](/Generateur-Devoirs/TS/ChapGeomSpace/ex114_c/73.png)
On a alors, dans le triangle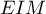 ,
,
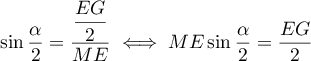 .
Or
.
Or 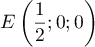 et
et 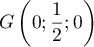 ,
d'où
,
d'où 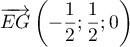 ,
et donc,
,
et donc, 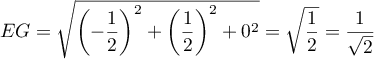 .
On obtient bien ainsi,
.
On obtient bien ainsi,
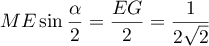 .
.
-
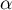 désigne la mesure en radians d'un angle géométrique,
et donc
désigne la mesure en radians d'un angle géométrique,
et donc ![$\alpha\in[0;\pi]](/Generateur-Devoirs/TS/ChapGeomSpace/ex114_c/82.png) .
On a alors
.
On a alors 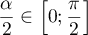 , intervalle sur
lequel la fonction sinus est croissante:
, intervalle sur
lequel la fonction sinus est croissante:
![\begin{tabular}{|c|ccc|}\hline
$\alpha$ & $0$ &\hspace*{1cm}& $\pi$ \\\hline
&&&$\dfrac\pi2$\\
$\dfrac\alpha2$ & &
\psline[arrowsize=7pt]{->}(-.7,-.4)(.8,.5)& \\
&0&&\\\hline
&&&1\\
$\sin\dfrac\alpha2$&&\psline[arrowsize=7pt]{->}(-.7,-.4)(.8,.5)&\\
&0&&\\\hline
\end{tabular}](/Generateur-Devoirs/TS/ChapGeomSpace/ex114_c/84.png)
On en déduit en particulier que: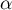 maximal
maximal 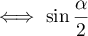 maximal.
maximal.
De plus, on a d'après la question précédente,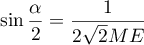 .
.
Donc,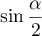 est maximal lorsque
est maximal lorsque 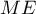 est minimal, et
donc lorsque
est minimal, et
donc lorsque 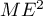 est minimal car la fonction carré étant
croissante sur
est minimal car la fonction carré étant
croissante sur  ,
, 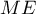 et
et 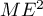 ont le même sens de
variation.
ont le même sens de
variation.
- On avait
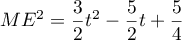 .
En notant
.
En notant 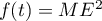 , on définit une fonction
, on définit une fonction 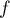 trinôme du
second degré, donc dérivable sur
trinôme du
second degré, donc dérivable sur 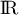 , et telle que
, et telle que
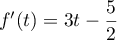 et qui est donc décroissante
sur
et qui est donc décroissante
sur ![$\Bigl[-\infty;\dfrac56\Bigl]](/Generateur-Devoirs/TS/ChapGeomSpace/ex114_c/99.png) et croissante sur
et croissante sur 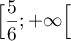 .
En particulier
.
En particulier  , donc
, donc  , donc aussi
, donc aussi 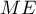 ,
a un minimum en
,
a un minimum en  .
.
La position du point telle que la mesure de l'angle soit
maximale est donc celle atteinte pour le paramètre
telle que la mesure de l'angle soit
maximale est donc celle atteinte pour le paramètre  ,
soit
,
soit 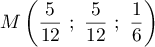 .
.
- Le point
Cacher la correction
Exercice 13: Bac 2010 - Représentation paramétrique, distance minimale
Bac S, septembre 2010 4 points
L'espace est rapporté à un repère orthonormal .
Soit
.
Soit  le plan d'équation :
le plan d'équation :  et
et  la droite dont une représentation paramétrique est
la droite dont une représentation paramétrique est

Bac S, septembre 2010 4 points
Cacher la correction
L'espace est rapporté à un repère orthonormal
 .
Soit
.
Soit  le plan d'équation :
le plan d'équation :  et
et  la droite dont une représentation paramétrique est
la droite dont une représentation paramétrique est

-
- Le point C(1 ; 3 ; 2) appartient-il au plan
 ? Justifier.
? Justifier.
- Démontrer que la droite
 est incluse dans le plan
est incluse dans le plan  .
.
- Le point C(1 ; 3 ; 2) appartient-il au plan
- Soit
 le plan passant par le point C et orthogonal à la droite
le plan passant par le point C et orthogonal à la droite  .
.
- Déterminer une équation cartésienne du plan
 .
.
- Calculer les coordonnées du point I, point d'intersection du plan
 et de la droite
et de la droite  .
.
- Montrer que CI
 .
.
- Déterminer une équation cartésienne du plan
- Soit
 un nombre réel et
un nombre réel et  le point de la droite
le point de la droite  de coordonnées
de coordonnées  .
.
- Vérifier que pour tout nombre réel
 .
.
- Montrer que CI est la valeur minimale de C
 lorsque
lorsque  décrit l'ensemble des nombres réels.
décrit l'ensemble des nombres réels.
- Vérifier que pour tout nombre réel
Correction exercice 13
Bac S, septembre 2010 4 points
-
-
C(1 ; 3 ; 2)
 , faux. Le point C n'appartient pas au plan
, faux. Le point C n'appartient pas au plan  .
.
-
Soit
 un point de
un point de  .
.
 , vrai quel que soit
, vrai quel que soit  .
.
Tout point de est un point de
est un point de  , donc la droite
, donc la droite  est incluse dans le plan
est incluse dans le plan  .
.
-
C(1 ; 3 ; 2)
-
-
Un vecteur normal au plan
 est un vecteur directeur de
est un vecteur directeur de  ; d'après la représentation paramétrique les coordonnées d'un vecteur directeur de
; d'après la représentation paramétrique les coordonnées d'un vecteur directeur de  sont
sont  .
.
Une équation du plan est donc :
est donc :
 .
.
Or C(1 ; 3 ; 2) .
.
Conclusion : .
.
-
Soit
 un point de
un point de  .
.
 .
.
Donc le point commun I à et à la droite
et à la droite  a pour coordonnées
a pour coordonnées  .
.
-
On a
 .
Donc CI
.
Donc CI .
.
Conclusion CI .
.
-
Un vecteur normal au plan
- Soit
 un nombre réel et
un nombre réel et  le point de la droite
le point de la droite  de coordonnées
de coordonnées  .
.
-
On calcule les coordonnées de
 soit
soit  .
On a
.
On a  .
.
-
 .
.
Le minimum de ce trinôme somme de deux carrés est obtenue lorsque le premier carré est nul soit pour et la valeur minimale de trinôme est égale à
et la valeur minimale de trinôme est égale à  . CI est bien la valeur minimale.
. CI est bien la valeur minimale.
-
On calcule les coordonnées de
Cacher la correction
Quelques autres devoirs
maison de géométrie plane: géométrie plane analytique, vecteurs et équations de droites, exponentielle, tangente
géométrie plane analytique, vecteurs et équations de droites, géométrie avec une hyperbole et ses tangentes, courbe représentative de la fonction inverse
géométrie dans l'espace, vecteurs et équations de plan, représentation paramétrique d&une droite de l'espace, tangente à une courbe, exponentielle
géométrie dans l'espace, vecteurs et équations de plan, représentation paramétrique d&une droite de l'espace, tangente à une courbe, exponentielle - Analyse: étude d'une fonction: variations, limites, TVI, asymptotes, ...
étude de la convexité de fonctions (et variations, tangentes, limites, ...) et géométrie dans l'espace
Quelques exercices corrigés
Exercices corrigés
Révisions dans le plan
Exercices corrigés
Bac 2024 (19 juin): Un peu de tout dans un tétraèdre
Exercices corrigés
Bac 2023 (20 mars): Un peu de tout dans l'espace
Exercices corrigés
Bac 2022 (12 mai): Un peu de tout dans l'espace
Exercices corrigés
Bac 2022 (11 mai): Un peu de tout dans l'espace
Voir aussi: