Bac 2014 - Suite d'intégrales et exponentielle
Exercice corrigé - Spécialité maths, terminale générale
Bac S, 19 juin 2014, 5 points
Partie A
Dans le plan muni d'un repère orthonormé, on désigne par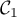 la courbe représentative de la fonction
la courbe représentative de la fonction 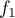 définie sur
définie sur 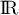 par:
par:
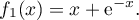
Partie B
L'objet de cette partie est d'étudier la suite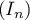 définie sur
définie sur 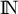 par:
par:
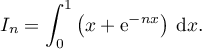
Correction
Partie A
Dans le plan muni d'un repère orthonormé, on désigne par
- Justifier que
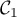 passe par le point A de coordonnées
passe par le point A de coordonnées 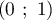 .
.
- Déterminer le tableau de variation de la fonction
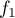 . On
précisera les limites de
. On
précisera les limites de 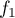 en
en 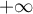 et en
et en 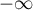 .
.
Partie B
L'objet de cette partie est d'étudier la suite
- Dans le plan muni d'un repère orthonormé
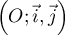 ,
pour tout entier
naturel
,
pour tout entier
naturel 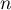 , on note
, on note 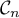 la courbe représentative de la
fonction
la courbe représentative de la
fonction 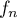 définie sur
définie sur 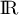 par
par
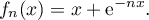
Sur le graphique ci-dessous on a tracé la courbe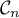 pour plusieurs valeurs de l'entier
pour plusieurs valeurs de l'entier 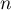 et la droite
et la droite 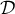 d'équation
d'équation 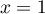 .
.
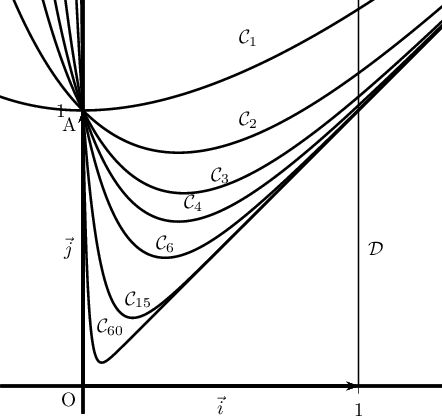
- Interpréter géométriquement l'intégrale
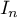 .
.
- En utilisant cette interprétation, formuler une conjecture sur
le sens de variation de la suite
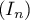 et sa limite
éventuelle. On précisera les éléments sur lesquels on s'appuie
pour conjecturer.
et sa limite
éventuelle. On précisera les éléments sur lesquels on s'appuie
pour conjecturer.
- Interpréter géométriquement l'intégrale
- Démontrer que pour tout entier naturel
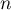 supérieur ou égal à 1,
supérieur ou égal à 1,
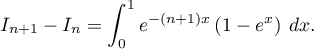
En déduire le signe de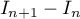 puis démontrer que la suite
puis démontrer que la suite
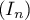 est convergente.
est convergente.
- Déterminer l'expression de
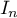 en fonction de
en fonction de 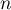 et
déterminer la limite de la suite
et
déterminer la limite de la suite 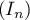 .
.
Correction
Tags:ExponentielleFonctionsIntégralesSuites
Voir aussi:
Quelques devoirs
maison de géométrie plane: géométrie plane analytique, vecteurs et équations de droites, exponentielle, tangente
géométrie dans l'espace, vecteurs et équations de plan, représentation paramétrique d&une droite de l'espace, tangente à une courbe, exponentielle
Bac blanc: QCM: fonctions, convexité, suite et programme Python - Probabilités: test pour détecter une maladie - Suites: un peu sur les suites - Géométrie dans l'espace - Fonction logarithme
logarithme népérien: résolution d'équations, étude de fonction, et convexité, points d'inflexion
maison: calculs de dérivées, limites, fonctions et suites récurrentes, démonstration par récurrence et théorème des gendarmes
