Suite de fonctions et d'intégrales, IPP
Exercice corrigé - Spécialité maths, terminale générale
-
On considère les suites
- Sont représentées ci-contre les fonctions
définies sur
l'intervalle 
par
pour différentes valeurs de
.
- Formuler une conjecture sur le sens de variation de la suite
en expliquant la démarche.
- Démontrer cette conjecture.
- Formuler une conjecture sur le sens de variation de la suite
-
- Montrer que pour tout entier
et pour tout nombre réel 
de l'intervalle [0~;~1] :
- Montrer que les suites
et
sont convergentes et déterminer leur limite.
- Montrer que pour tout entier
-
- Montrer, en effectuant une intégration par parties, que pour
tout entier
:
- En déduire
.
- Montrer, en effectuant une intégration par parties, que pour
tout entier
et 
définies pour tout entier naturel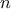 
par:
Correction
Tags:IntégralesSuitesExponentielle
Autres sujets au hasard:
Voir aussi: