Suite de fonctions et d'intégrales, IPP
Exercice corrigé - Spécialité maths, terminale générale
-
On considère les suites
- Sont représentées ci-contre les fonctions
 définies sur
l'intervalle
définies sur
l'intervalle  par
par

pour différentes valeurs de .
.
- Formuler une conjecture sur le sens de variation de la suite
 en expliquant la démarche.
en expliquant la démarche.
- Démontrer cette conjecture.

- Formuler une conjecture sur le sens de variation de la suite
-
- Montrer que pour tout entier
 et pour tout nombre réel
et pour tout nombre réel  de l'intervalle [0~;~1] :
de l'intervalle [0~;~1] :

- Montrer que les suites
 et
et
 sont convergentes et déterminer leur limite.
sont convergentes et déterminer leur limite.
- Montrer que pour tout entier
-
- Montrer, en effectuant une intégration par parties, que pour
tout entier
 :
:

- En déduire
 .
.
- Montrer, en effectuant une intégration par parties, que pour
tout entier
 et
et  définies pour tout entier naturel
définies pour tout entier naturel 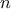 par:
par:

Correction
Cacher la correction
-
- Les fonctions représentées sont positives ;
 représente
donc l'aire de la surface limitée par le représentation de
représente
donc l'aire de la surface limitée par le représentation de
 , l'axe des abscisses et les droites d'équations
, l'axe des abscisses et les droites d'équations  et
et
 . Le dessin suggère que la suite
. Le dessin suggère que la suite  est
décroissante.
est
décroissante.
-
 .
.
Or (par croissance de la fonction exponentielle)
(par croissance de la fonction exponentielle)
 .
En multipliant chaque membre de cette dernière inégalité par
.
En multipliant chaque membre de cette dernière inégalité par
 , on obtient:
, on obtient:
 ,
soit finalement:
,
soit finalement:
 .
.
Par intégration sur l'intervalle [0~;~1] des fonctions continues et
et  :
:
 :
la suite
:
la suite  est décroissante.
est décroissante.
- Les fonctions représentées sont positives ;
-
-
 et par produit par le nombre positif
et par produit par le nombre positif  ,
on obtient:
,
on obtient:
 .
.
D'autre part on sait que pour , on a
, on a 

et par produit par le nombre positif , on obtient:
, on obtient:
 .
.
Enfin on a ,
donc finalement :
,
donc finalement :

- Par intégration sur l'intervalle
 des inégalités
précédentes on obtient
des inégalités
précédentes on obtient

soit encore:
c'est à dire: .
.
Or ,
donc
,
donc  .
.
On peut donc conclure, d'après le théorème des gendarmes, que les suites et
et  convergent vers
convergent vers  .
.
-
-
- Posons

Toutes ces fonctions sont continues car dérivables sur ;
en intégrant par parties on a donc:
;
en intégrant par parties on a donc:
 ;
;
 ou encore
ou encore

- Le résultat précédent peut s'écrire en multipliant par
 :
:
 .
.
Comme ,
on a donc :
,
on a donc :

Remarque : on a donc pour assez grand
assez grand
 .
.
Exemple : pour , la calculatrice donne
, la calculatrice donne  .
.
- Posons
Cacher la correction
Tags:IntégralesSuitesExponentielle
Voir aussi:
