Oral de Bac - Intersection et distance entre un plan (équation cartésienne) et une droite (représentée paramétriquement)
Exercice corrigé - Spécialité maths, terminale générale
Dans l'espace muni du repère orthonormal 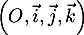 on considère le plan
on considère le plan 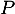 d'équation
d'équation
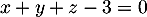 ainsi que le point
ainsi que le point 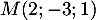 .
.
- Le point
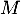 est-il dans le plan
est-il dans le plan 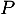 ?
?
- Donner une représentation paramétrique de la droite
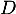 passant
par
passant
par 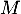 et orthogonale à
et orthogonale à 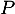 .
.
- Déterminer les coordonnées du point
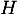 intersection de
intersection de 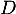 et
et 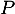 .
.
- En déduire la distance du point
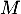 au plan
au plan 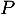 .
.
Correction
Cacher la correction
-
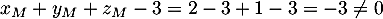 donc
donc 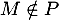 .
.
-
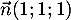 est un vecteur normal de
est un vecteur normal de 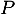 ,
la droite
,
la droite 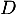 passant par
passant par 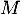 et orthogonale à
et orthogonale à 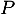 admet donc
comme représentatation paramétrique:
admet donc
comme représentatation paramétrique:
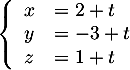
- Comme
 , il existe un réel
, il existe un réel  tel que
tel que 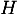 ait pour
coordonnées
ait pour
coordonnées
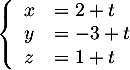 Comme de plus
Comme de plus 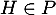 , ses coordonnées vérifient l'équation de
, ses coordonnées vérifient l'équation de 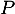 donc
donc 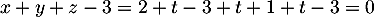 ,
soit
,
soit 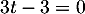 et donc
et donc 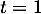 .
.
On a ainsi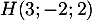 .
.
- La distance du point
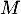 au plan
au plan 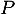 est
est 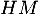 .
Comme
.
Comme 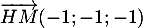 , on a donc
, on a donc 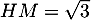 .
.
Cacher la correction
Tag:Géométrie dans l'espace
Voir aussi:
