Équation différentielle du premier ordre
Exercice corrigé - Spécialité maths, terminale générale
On considère l'équation différentielle
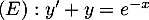 .
.
- Montrer que la fonction
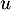 définie sur
définie sur 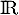 par
par
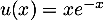 est une solution de l'équation différentielle
est une solution de l'équation différentielle 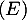 .
.
- On considère l'équation différentielle
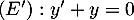 .
Résoudre l'équation différentielle
.
Résoudre l'équation différentielle 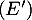 .
.
- En déduire toutes les solutions de l'équation différentielle
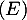 .
.
- Déterminer l'unique solution
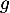 de l'équation différentielle
de l'équation différentielle 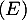 telle que
telle que 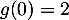 .
.
- Étudier la convexité de
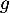 sur
sur 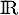 .
.
Correction
D'après Bac S, métropole, 22 juin 2010
On considère l'équation différentielle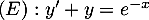 .
.
Cacher la correction
D'après Bac S, métropole, 22 juin 2010
On considère l'équation différentielle
-
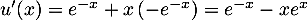 et donc
et donc
![\[u'(x)+u(x)=e^{-x}-xe^{x}+xe^{-x}=e^{-x}\]](/Generateur-Devoirs/TS/ChapEqDiff/excours_c/3.png)
ce qui montre que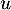 est bien solution de
est bien solution de 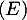 .
.
- Les solutions de
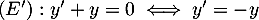 sont les fonctions définies par
sont les fonctions définies par
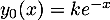 , pour tout réel
, pour tout réel 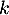 .
.
- Les solutions de l'équation différentielle
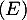 sont alors
sont alors
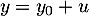 , soit, pour tout réel
, soit, pour tout réel 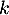 ,
,
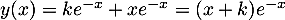 .
.
-
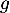 est une solution, donc
est une solution, donc 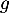 s'écrit sous la forme
s'écrit sous la forme
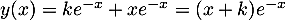 .
.
De plus,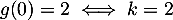 ,
d'où
,
d'où 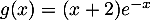 .
.
-
![\[g'(x)=-g(x)+e^{-x}=-(x+2)e^{-x}+e^{-x}=-(x+1)e^{-x}\]](/Generateur-Devoirs/TS/ChapEqDiff/excours_c/18.png)
Pour calculer la dérivée seconde, on peut soit dériver à nouveau ce produit, soit utiliser l'équation différentielle. Comme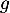 est solution de
est solution de 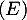 , on a
, on a
![\[g'(x)=-g(x)+e^{-x}\]](/Generateur-Devoirs/TS/ChapEqDiff/excours_c/21.png)
et donc, en dérivant
![\[g''(x)=-g'(x)-e^{-x}\]](/Generateur-Devoirs/TS/ChapEqDiff/excours_c/22.png)
soit,
![\[g''(x)=(x+1)e^{-x}-e^{-x}=xe^{-x}\]](/Generateur-Devoirs/TS/ChapEqDiff/excours_c/23.png)
Comme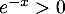 pour tout réel
pour tout réel 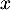 , on obtient donc
que pour
, on obtient donc
que pour 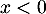 ,
, 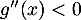 et donc
et donc 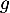 est concave,
et pour
est concave,
et pour 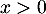 ,
, 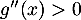 et donc
et donc 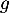 est convexe.
est convexe.
Enfin la courbe de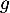 admet un unique point d'inflexion en
admet un unique point d'inflexion en 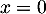 .
.
Cacher la correction
Tag:Équations différentielles
Voir aussi:
Quelques devoirs
sur les équations différentielles: désintégration de noyaux radioactifs - Température de refroidissement d'un objet (Bac S, Antilles-Guyane, 23 juin 2009) - Équaton différentielle avec changement de fonction (Bac S, métropole, 22 juin 2010) - Équaton différentielle non linéaire, avec un carré
Primitives, vérification qu'une fonction donnée est solution d'une équation différentielle, étude de fonction et de convexité
Primitives, vérification qu'une fonction donnée est solution d'une équation différentielle, étude de fonction et de convexité - Probabilités & loi binomiale - Suite récurrente
sur la résolution d'&quations différentielles
