Bac 2009 (Antilles-Guyane): Équation différentielle, exponentielle, suite
Exercice corrigé - Spécialité maths, terminale générale
La température de refroidissement d'un objet fabriqué industriellement
est une fonction  du temps
du temps 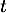 .
Cette fonction
.
Cette fonction 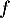 est définie sur l'ensemble des nombres réels positifs et vérifie
l'équation différentielle:
est définie sur l'ensemble des nombres réels positifs et vérifie
l'équation différentielle:
![\[y'(t)+\dfrac12y(t)=10\]](/Generateur-Devoirs/TS/ChapEqDiff/exAG2009/4.png)
La température est exprimée en degrés Celsius ( C)
et le temps
C)
et le temps 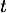 en heures.
en heures.
Correction
La température est exprimée en degrés Celsius (
- Déterminer
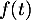 pour
pour  , sachant que pour
, sachant que pour  ,
la température de l'objet est 220
,
la température de l'objet est 220  C.
C.
- Pour la suite, on prendra comme fonction
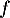 ,
la fonction suivante définie sur
,
la fonction suivante définie sur  par
par
![\[f(t)=200e^{-\frac{t}2}+20\]](/Generateur-Devoirs/TS/ChapEqDiff/exAG2009/13.png)
On note sa courbe représentative.
sa courbe représentative.
- Étudier les variations de la fonction
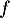 sur
sur 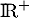 .
.
- Étudier la limite de la fonction
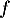 en
en 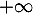 .
La courbe
.
La courbe 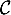 admet-elle une asymptote en
admet-elle une asymptote en 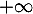 ?
?
- Représenter graphiquement
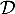 .
.
- Étudier les variations de la fonction
- Déterminer le moment où la température de l'objet est 50
 C.
C.
Donner une valeur approchée de ce moment en heures et minutes.
Correction
Tag:Équations différentielles
Voir aussi:
Quelques devoirs
sur les équations différentielles: désintégration de noyaux radioactifs - Température de refroidissement d'un objet (Bac S, Antilles-Guyane, 23 juin 2009) - Équaton différentielle avec changement de fonction (Bac S, métropole, 22 juin 2010) - Équaton différentielle non linéaire, avec un carré
Primitives, vérification qu'une fonction donnée est solution d'une équation différentielle, étude de fonction et de convexité
Primitives, vérification qu'une fonction donnée est solution d'une équation différentielle, étude de fonction et de convexité - Probabilités & loi binomiale - Suite récurrente
sur la résolution d'&quations différentielles
