Calculs d'intégrales

Exercice corrigé - Spécialité maths, terminale générale

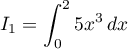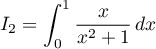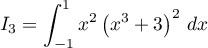
Calculer les intégrales: $I_1=\dsp\int_0^25x^3\,dx$ ; $I_2=\dsp\int_0^1\dfrac{x}{x^2+1}\,dx$ ; $I_3=\dsp\int_{-1}^1 x^2\left( x^3+3\rp^2\,dx$
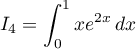
À l'aide d'une intégration par parties, calculer $I_4=\dsp\int_0^1xe^{2x}\,dx$

Correction
$I_1=\dsp\int_0^25x^3\,dx=\lb\dfrac54x^4\right] =\dfrac54\tm2^4-0=20$
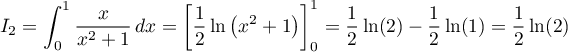
$I_2=\dsp\int_0^1\dfrac{x}{x^2+1}\,dx =\lb\dfrac12\ln\left( x^2+1\rp\rb_0^1 =\dfrac12\ln(2)-\dfrac12\ln(1)=\dfrac12\ln(2)$
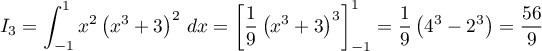
$I_3=\dsp\int_{-1}^1 x^2\left( x^3+3\rp^2\,dx =\lb\dfrac19\left( x^3+3\rp^3\rb_{-1}^1 =\dfrac19\lp4^3-2^3\right) =\dfrac{56}9$
En intégrant par parties, en posant

et $v'=e^{2x}$ , donc

et $v=\frac12e^{2x}$ ,

$\begin{array}{ll}I_4&=\dsp\int_0^1xe^{2x}\,dx\\[1em] &=\left[ \dfrac12xe^{2x}\rb_0^1-\dsp\int_0^1\dfrac12e^{2x}\,dx\\[1em] &=\dfrac12e^2-\lb\dfrac14e^{2x}\rb_0^1\\[1em] &=\dfrac12e^2-\lp\dfrac14e^2-\dfrac14e^0\rp\\[1em] &=\dfrac14e^2+\dfrac14 \enar$

Cacher la correction

Tag:Intégrales

Autres sujets au hasard:

Voir aussi: